按顺序给出若干个矩形的高度和宽度。每个矩形放置在地面上紧贴着。
例如一个$1\times 1$和$2\times 2$的矩形如下。
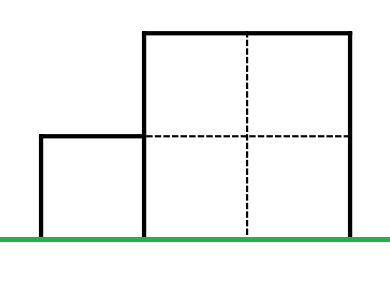
求给出的图形的所有可能的子矩形的个数。只要子矩形形状或位置不一样则认为子矩形不同。
例如在上图中
有5个

有3个
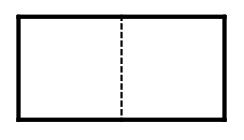
有1个
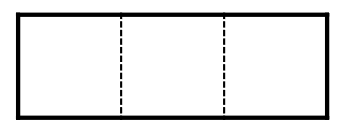
有2个
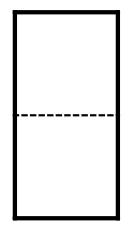
有1个
共计12个。
">Fancy Fence
Fancy Fence
Created by LXC on Tue Sep 19 09:10:02 2023
https://codeforces.com/problemset/problem/1402/A
ranting: 1800
tag: *special, data structures, dsu, implementation, math, sortings
problem
按顺序给出若干个矩形的高度和宽度。每个矩形放置在地面上紧贴着。
例如一个$1\times 1$和$2\times 2$的矩形如下。

求给出的图形的所有可能的子矩形的个数。只要子矩形形状或位置不一样则认为子矩形不同。
例如在上图中
有5个

有3个

有1个

有2个

有1个

共计12个。
solution
考虑所有矩形的子矩形的个数。一个$h\times w$的矩形可以找到$\frac{h(h+1)}{2} \times \frac{w(w+1)}{2}$个子矩形。
此外,对于一个矩形高度固定的情况下左右两侧能延申,延申得到最大宽度,形成一个新的矩形可以在其中寻找子矩形。
设$f(x) = \frac{x(x+1)}{2}$,答案就是$\sum\limits_{i=1}^n f(w_i) \times f(h_i)+\sum\limits_{1\leq l<r\leq n} w_lw_rf(\min\limits_{i=l}^r(h_i))$
对于$\sum\limits_{1\leq l<r\leq n} w_lw_rf(\min\limits_{i=l}^r(h_i))$直接计算时间复杂度$O(n^2)$,需要优化。
我们可以用单调栈$O(n)$预处理每个矩形高度$h_i$:左侧最近的一个高度严格小于当前高度的位置$l_i$,以及右侧最近一个高度小于等于当前高度的位置$r_i$。如果两个都是严格小于将会有计数重复。
$\sum \limits_{i=1}^{n} h_i\left[ \sum\limits_{j = l_i+1}^{i}w_j \times \sum\limits_{j = i}^{r_i-1}w_j-w_i^2 \right]$
$\sum w$可以用前缀数组预处理,求区间和只需$O(1)$,此和式计算只需$O(n)$。
code
1 |
|