1631. 最小体力消耗路径
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上 ,下 ,左 ,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
```txt
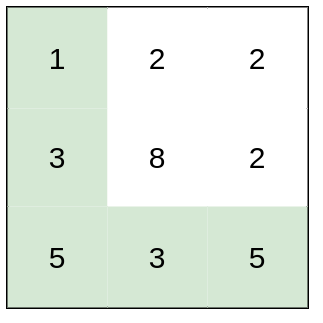
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
```
示例 2:
```txt
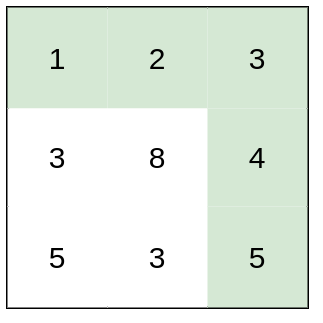
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
```
示例 3:
```txt
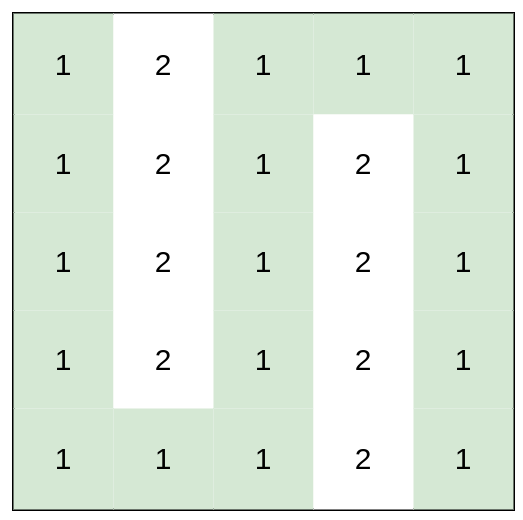
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
```
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6
题目 1631. 最小体力消耗路径
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上 ,下 ,左 ,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
1 2 3 4 输入:heights = [[1,2,2],[3,8,2],[5,3,5]] 输出:2 解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。 这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
1 2 3 输入:heights = [[1,2,3],[3,8,4],[5,3,5]] 输出:1 解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
1 2 3 输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]] 输出:0 解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6
题解 方法一: 思路 二分法。
若d为体力消耗值,则大于d的体力消耗值也能从起点到终点。所以找到最小的使得能从起点到达终点的d便是答案。
可以用dfs或bfs来判断能否从起点能到终点。
时间复杂度$O(m \cdot n \cdot logh)$ n为矩阵的行数,m为矩阵的列数,h为矩阵中的最大值。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : vector<vector<int >> g; int n, m; int vis[104 ][104 ]; int dfs (int x, int y, int d) vis[x][y] = 1 ; if (x == n-1 && y == m-1 ) return true ; for (int i=0 ; i<4 ; i++) { int mx = x + (i-1 )%2 ; int my = y + (i-2 )%2 ; if (mx<0 || mx>=n || my<0 || my>=m || vis[mx][my] || abs (g[x][y]-g[mx][my])>d) continue ; if (dfs (mx, my, d)) return true ; } return false ; } int minimumEffortPath (vector<vector<int >>& heights) n = heights.size (); m = heights[0 ].size (); g = heights; int l = 0 , r = 1e6 ; while (l < r) { int d = l+r>>1 ; memset (vis, 0 , sizeof (vis)); if (dfs (0 ,0 ,d)) { r = d; } else { l = d+1 ; } } return r; } };
方法二: 思路 并查集。
类似求最小生成树,可以把矩阵看作一个图,每个格子为图中的节点。相邻格子间存在一条边,边权为格子值之差的绝对值,先把所有边按照边权从小到大排序。再枚举每条边,将边所连接的两个点纳入同一个集合中,并判断起点与终点是否在同一集合,若在则当前所枚举的边权是路径中的最大值。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : int n, m; int st[10005 ]; int ufind (int x) if (st[x] < 0 ) return x; return st[x] = ufind (st[x]); } int to_id (int x, int y) return x*m+y; } int minimumEffortPath (vector<vector<int >>& g) n = g.size (), m = g[0 ].size (); if (0 == m*n-1 ) return 0 ; vector<vector<int >> e; for (int i=0 ; i<n; i++) { for (int j=1 ; j<m; j++) { e.push_back ({abs (g[i][j-1 ]-g[i][j]), to_id (i, j-1 ), to_id (i, j)}); } } for (int i=0 ; i<m; i++) { for (int j=1 ; j<n; j++) { e.push_back ({abs (g[j-1 ][i]-g[j][i]), to_id (j-1 , i), to_id (j, i)}); } } sort (e.begin (), e.end ()); memset (st, -1 , sizeof (st)); for (int i=0 ; i<e.size (); i++) { int x = ufind (e[i][1 ]), y = ufind (e[i][2 ]); if (x != y) { st[x] = y; } if (ufind (0 ) == ufind (n*m-1 )) return e[i][0 ]; } return -1 ; } };
方法三: 思路 djkstra
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public : int n, m; int dis[10005 ]; struct Node { int id, dis; bool operator <(const Node& o) const { return dis > o.dis; } }; int to_id (int x, int y) return x*m+y; } int minimumEffortPath (vector<vector<int >>& g) n = g.size (), m = g[0 ].size (); memset (dis, 0x3f , sizeof (dis)); dis[0 ] = 0 ; priority_queue<Node> que; que.push ({0 , 0 }); while (!que.empty ()) { auto u = que.top (); que.pop (); if (u.id == n*m-1 ) return u.dis; for (int i=0 , x=u.id/m, y = u.id%m; i<4 ; i++) { int dx = x+(i-1 )%2 ; int dy = y+(i-2 )%2 ; int id = to_id (dx, dy); if (dx<0 || dx>=n || dy<0 || dy>=m || dis[id] <= max (dis[u.id], abs (g[x][y]-g[dx][dy]))) continue ; dis[id] = max (dis[u.id], abs (g[x][y]-g[dx][dy])); que.push ({id, dis[id]}); } } return -1 ; } };