逃离火灾

发表于 更新于 分类于

    2258. 逃离火灾

    给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，它表示一个网格图。每个格子为下面 3 个值之一：

    • 0 表示草地。

    • 1 表示着火的格子。

    • 2 表示一座墙，你跟火都不能通过这个格子。

    一开始你在最左上角的格子 (0, 0) ，你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟，你可以移动到 相邻 的草地格子。每次你移动 之后 ，着火的格子会扩散到所有不是墙的 相邻 格子。

    请你返回你在初始位置可以停留的 最多 分钟数，且停留完这段时间后你还能安全到达安全屋。如果无法实现，请你返回 -1 。如果不管你在初始位置停留多久，你 总是 能到达安全屋，请你返回 10^9 。

    注意，如果你到达安全屋后，火马上到了安全屋，这视为你能够安全到达安全屋。

    如果两个格子有共同边，那么它们为 相邻 格子。

    示例 1：

    ```txt

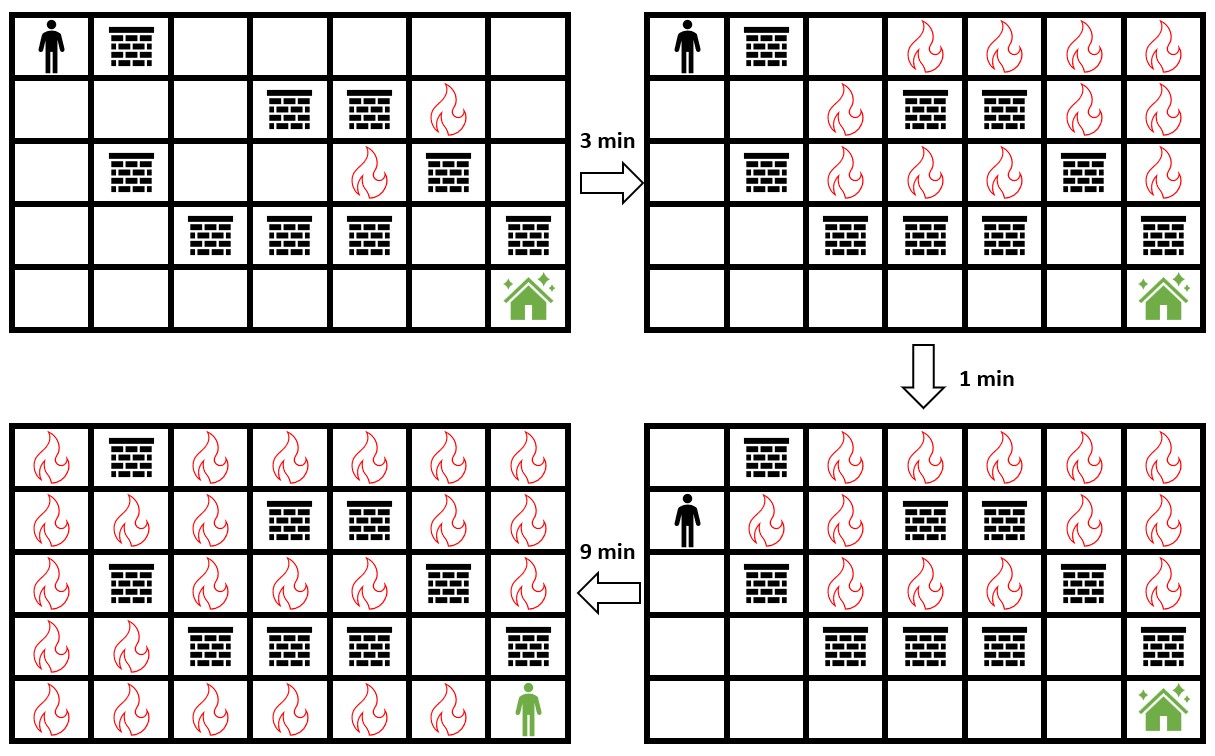
    输入：grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]

    输出：3

    解释：上图展示了你在初始位置停留 3 分钟后的情形。

    你仍然可以安全到达安全屋。

    停留超过 3 分钟会让你无法安全到达安全屋。

    ```

    示例 2：

    ```txt

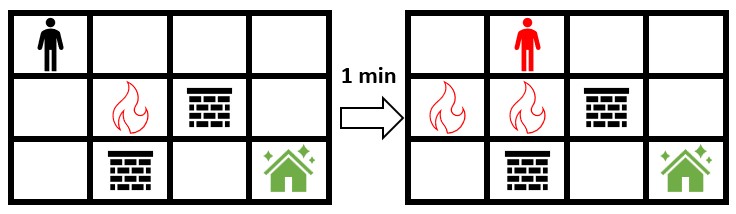
    输入：grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]

    输出：-1

    解释：上图展示了你马上开始朝安全屋移动的情形。

    火会蔓延到你可以移动的所有格子，所以无法安全到达安全屋。

    所以返回 -1 。

    ```

    示例 3：

    ```txt

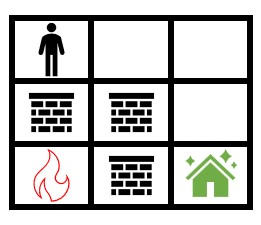
    输入：grid = [[0,0,0],[2,2,0],[1,2,0]]

    输出：1000000000

    解释：上图展示了初始网格图。

    注意，由于火被墙围了起来，所以无论如何你都能安全到达安全屋。

    所以返回 109 。

    ```

    提示：

    • m == grid.length

    • n == grid[i].length

    • 2 <= m, n <= 300

    • 4 <= m * n <= 2 * 10^4

    • grid[i][j] 是 0 ，1 或者 2 。

    • grid[0][0] == grid[m - 1][n - 1] == 0

题目

2258. 逃离火灾

给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，它表示一个网格图。每个格子为下面 3 个值之一：

  • 0 表示草地。
  • 1 表示着火的格子。
  • 2 表示一座墙，你跟火都不能通过这个格子。

一开始你在最左上角的格子 (0, 0) ，你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟，你可以移动到 相邻 的草地格子。每次你移动 之后 ，着火的格子会扩散到所有不是墙的 相邻 格子。

请你返回你在初始位置可以停留的 最多 分钟数，且停留完这段时间后你还能安全到达安全屋。如果无法实现，请你返回 -1 。如果不管你在初始位置停留多久，你 总是 能到达安全屋，请你返回 10^9 。

注意，如果你到达安全屋后，火马上到了安全屋，这视为你能够安全到达安全屋。

如果两个格子有共同边，那么它们为 相邻 格子。

示例 1：

1
2
3
4
5
输入：grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
输出：3
解释：上图展示了你在初始位置停留 3 分钟后的情形。
你仍然可以安全到达安全屋。
停留超过 3 分钟会让你无法安全到达安全屋。

示例 2：

1
2
3
4
5
输入：grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
输出：-1
解释：上图展示了你马上开始朝安全屋移动的情形。
火会蔓延到你可以移动的所有格子，所以无法安全到达安全屋。
所以返回 -1 。

示例 3：

1
2
3
4
5
输入：grid = [[0,0,0],[2,2,0],[1,2,0]]
输出：1000000000
解释：上图展示了初始网格图。
注意，由于火被墙围了起来，所以无论如何你都能安全到达安全屋。
所以返回 109 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 300
  • 4 <= m * n <= 2 * 10^4
  • grid[i][j] 是 0 ，1 或者 2 。
  • grid[0][0] == grid[m - 1][n - 1] == 0

题解

人在到达安全屋前不能遇到火，但可以和火同时到达安全屋。

方法一：

思路

两次bfs

进入终点最多有两个方向，终点上方和终点左方。

火和人在最后到达终点方向不同，求解的方式不同。

当火和人到达终点方向相同，答案是人到达终点的时间-火到达终点的时间-1；

当火和人到达终点方向不相同，答案是人到达终点的时间-火到达终点的时间。

为什么会这样？我是这样理解的：

人可以和火同时到达安全屋，当入屋的方向不同时，可以认为 人到达终点的路径 和 火到达终点的路径 在到达终点之前不会有重合，所以人和火可以同时到达终点。如果有重合那么人必须要赶在火之前到达终点，所以等待的时间要减1。

我们可以判断人与火在到达终点上方和终点左方的时间来确定答案。

这种边角情况很复杂。因为人可能在两个方向进入终点都是最短路径。对于火也有这种可能。

这里分三种情况考虑。

  • 当火的两个方向路径都是最短时，人无论如何都与火同路。
  • 当火不同，人相同时，人可以选择与火不同的一条路。
  • 当人火两个入口路径都不同时，看人与火是否同路。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#define INF 0x3f3f3f3f
class Solution {
public:
    int v1[305][305];
    int v2[305][305];
    int dx[4] = {0, 1, 0, -1};
    int dy[4] = {1, 0, -1, 0};
    struct Node {
        int x, y;
    };
    int maximumMinutes(vector<vector<int>>& g) {
        int n = g.size();
        int m = g[0].size();
        memset(v1, 0x3f, sizeof(v1));
        memset(v2, 0x3f, sizeof(v2));
        queue<Node> f, p;
        for (int i=0; i<n; i++) {
            for (int j=0; j<m; j++) {
                if (g[i][j] == 1) {
                    f.push({i, j});
                    v2[i][j] = 0;
                }
            }
        }
        while (!f.empty()) {
            auto u = f.front(); f.pop();
            for (int i=0; i<4; i++) {
                int x = dx[i] + u.x;
                int y = dy[i] + u.y;
                if (x<0 || x>=n || y<0 || y>= m || g[x][y] == 2) continue;
                if (v2[u.x][u.y]+1 < v2[x][y]) {
                    v2[x][y] = v2[u.x][u.y]+1;
                    f.push({x, y});
                }
            }
            
        }
        p.push({0,0});
        v1[0][0] = 0;
        while (!p.empty()) {
            auto u = p.front(); p.pop();
            for (int i=0; i<4; i++) {
                int x = dx[i] + u.x;
                int y = dy[i] + u.y;
                if (x<0 || x>=n || y<0 || y>= m || g[x][y] == 2) continue;
                if (v1[u.x][u.y]+1 < v1[x][y]) {
                    v1[x][y] = v1[u.x][u.y]+1;
                    p.push({x, y});
                }
            }
            
        }
        if (v1[n-1][m-1] == INF) return -1;//人与安全屋被墙分隔
        if (v2[n-1][m-1] == 0x3f3f3f3f) return 1e9;//人能到达安全屋, 但火和安全屋被墙阻隔。
        int a1 = v1[n-2][m-1], a2 = v1[n-1][m-2];//人到达两个入口的最短时间
        int b1 = v2[n-2][m-1], b2 = v2[n-1][m-2];//火到达两个入口的最短时间
        // cout << a1 << " " << a2 << endl;
        // cout << b1 << " " << b2 << endl;
        int add;
        if (b1 == b2) {//无论人怎么选，人与火必定同路
            add = 1;
        } else if (a1 == a2) {//人可以选择与火不同的入口
            add = 0;
        } else if (a1 < a2 && b1 < b2 || a1 > a2 && b1 > b2) {//选最小值作为最短路，同方向进入安全屋
            add = 1;
        } else add = 0;
        // cout << add << endl;
        if (v2[n-1][m-1] - v1[n-1][m-1] - add < 0) return -1;
        return v2[n-1][m-1] - v1[n-1][m-1] - add;
    }
};

方法二：

思路

二分思路

可以先让火的bfs得到火到任意点的最短时间。

然后二分时用人的bfs是否能到达安全屋作为判断条件。随着等待的时间增大，到达安全屋的结果由 能 变为 不能。可以找到第一个不能到达的等待时间再减一便可得到答案。

如何通过人的bfs来判断是否能到达安全屋呢？

保证两个条件：

人在到达安全屋前不能遇到火，但可以和火同时到达安全屋。

所以人bfs时，只有当人的到达某个非终点单元格的时间小于火到达该单元格的时间才能入队列。这样就保证人在到达安全屋前不能遇到火。

然后对于人和火可以同时到达安全屋，这一条件须要在入队列前判断是否到达终点，因为人和火是可以同时到达终点的，而从队列里出来的人是严格小于火的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int fire[303][303], peo[303][303];
    int maximumMinutes(vector<vector<int>>& g) {
        int n = g.size(), m = g[0].size();
        memset(fire, 0x3f, sizeof(fire));
        queue<pair<int,int>> q;
        for (int i=0; i<n; i++) {
            for (int j=0; j<m; j++) {
                if (g[i][j] == 1) {
                    q.emplace(i,j);
                    fire[i][j] = 0;
                }
            }
        }
        while (q.size()) {
            auto [x, y] = q.front(); q.pop();
            for (int i=0; i<4; i++) {
                int dx = x + (i-1)%2;
                int dy = y + (i-2)%2;
                if (dx < 0 || dx >= n || dy < 0 || dy >= m || g[dx][dy] == 2) continue;
                if (fire[dx][dy] > fire[x][y]+1) {
                    fire[dx][dy] = fire[x][y]+1;
                    q.emplace(dx, dy);
                }
            }
        }
        // for (int i=0; i<n; i++) {
        //     for (int j=0; j<m; j++) {
        //         cout << fire[i][j] << " ";
        //     } cout << endl;
        // }
        long l = 0, r = 1e9+1;
        while (l<r) {
            long o = l+r>>1;
            while (q.size()) q.pop();
            q.emplace(0,0);
            memset(peo, 0x3f, sizeof(peo));
            peo[0][0] = o;
            while (q.size()) {
                auto [x, y] = q.front(); q.pop();
                for (int i=0; i<4; i++) {
                    int dx = x + (i-1)%2;
                    int dy = y + (i-2)%2;
                    if (dx < 0 || dx >= n || dy < 0 || dy >= m || g[dx][dy] == 2) continue;
                    if (fire[dx][dy] >= peo[x][y]+1 && peo[dx][dy] > peo[x][y]+1) {
                        if (fire[dx][dy] > peo[x][y]+1 || dx == n-1 && dy == m-1) {
                            peo[dx][dy] = peo[x][y]+1;
                            q.emplace(dx, dy);
                        }
                    }
                }
            }
            if (peo[n-1][m-1] == INF) {
                r = o;
            } else {
                l = o+1;
            }
        }
        return r-1; //r第一个不可到达的时间点。
    }
};