树中可以形成回文的路径数

题目

2791. 树中可以形成回文的路径数

---

给你一棵 树（即，一个连通、无向且无环的图），根 节点为 0 ，由编号从 0 到 n - 1 的 n 个节点组成。这棵树用一个长度为 n 、下标从 0 开始的数组 parent 表示，其中 parent[i] 为节点 i 的父节点，由于节点 0 为根节点，所以 parent[0] == -1 。

另给你一个长度为 n 的字符串 s ，其中 s[i] 是分配给 i 和 parent[i] 之间的边的字符。s[0] 可以忽略。

找出满足 u < v ，且从 u 到 v 的路径上分配的字符可以 重新排列 形成 回文 的所有节点对 (u, v) ，并返回节点对的数目。

如果一个字符串正着读和反着读都相同，那么这个字符串就是一个 回文 。

示例 1：

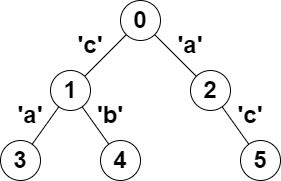
输入：parent = [-1,0,0,1,1,2], s = "acaabc"
输出：8
解释：符合题目要求的节点对分别是：
- (0,1)、(0,2)、(1,3)、(1,4) 和 (2,5) ，路径上只有一个字符，满足回文定义。
- (2,3)，路径上字符形成的字符串是 "aca" ，满足回文定义。
- (1,5)，路径上字符形成的字符串是 "cac" ，满足回文定义。
- (3,5)，路径上字符形成的字符串是 "acac" ，可以重排形成回文 "acca" 。

示例 2：

输入：parent = [-1,0,0,0,0], s = "aaaaa"
输出：10
解释：任何满足 u < v 的节点对 (u,v) 都符合题目要求。

提示：

• n == parent.length == s.length
• 1 <= n <= 10^5
• 对于所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
• parent[0] == -1
• parent 表示一棵有效的树
• s 仅由小写英文字母组成

题解

方法一：

思路

我们要求任意两点之间的路径，路径上字符可以重组形成回文串的点对数。

回文串只需要让路径上字符出现次数为奇数的个数不超过1就行。

也就是说每个字符出现的次数并不关心，只关心出现的次数的奇偶性，而字符的个数是小写英文字母，共计26个。可以用26位的二进制数表示每个字符出现的奇偶性。

我们可以将任意两个点之间的路径看作，这俩个点分别到根节点的路径拼接而成。但是任意两点之间的路径有些不含根节点，如果硬是要经过根节点，则可以看作经过两次公共祖先到根节点的路径。经过两次则可以认为公共祖先到根节点的路径不会影响答案。这可以用异或运算巧妙实现。

我们先处理出任意点i到根的所有字母奇偶性$a_i$。

由小到大遍历节点，对于节点i，假设已经将比i小的节点j的$a_j$存入哈希表，然后从哈希表选取一个值x使得$x\oplus a_i = y$，$y$最多只存在一个比特位为1。显然y的取值只有27种，之际枚举y，然后查询哈希表$y\oplus a_i$的个数累加到答案，即可得到以i为第二关键字的点对(j,i)的所有点对数。

代码

class Solution {
public:
    using ll = long long;
    long long countPalindromePaths(vector<int>& parent, string s) {
        int n = parent.size();
        vector<int> a(n, -1);
        for (int i=0; i<n; i++) {
            int p = i, cur = 0;
            while (p != 0) {
                if (a[p] != -1) {
                    cur ^= a[p];
                    break;
                } 
                cur ^= 1<<(s[p]-'a');
                p = parent[p];
            }
            a[i] = cur;
            // cout << i << " " << a[i] << "\n";
        }
        map<int,ll> mp;
        ll ans = 0;
        for (int i=0; i<n; i++) {
            if (mp.count(a[i])) ans += mp[a[i]];
            for (int j=0; j<26; j++) {
                if (mp.count(a[i]^(1<<j))) ans += mp[a[i]^(1<<j)];
            }
            mp[a[i]]++;
        }
        return ans;

    }
};