边权重均等查询

发表于 更新于 分类于

    2846. 边权重均等查询

    现有一棵由 n 个节点组成的无向树，节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。

    另给你一个长度为 m 的二维整数数组 queries ，其中 queries[i] = [ai, bi] 。对于每条查询，请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中，你可以选择树上的任意一条边，并将其权重更改为任意值。

    注意：

    • 查询之间 相互独立 的，这意味着每条新的查询时，树都会回到 初始状态 。

    • 从 ai 到 bi的路径是一个由 不同 节点组成的序列，从节点 ai 开始，到节点 bi 结束，且序列中相邻的两个节点在树中共享一条边。

    返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 条查询的答案。

    示例 1：

    ```txt

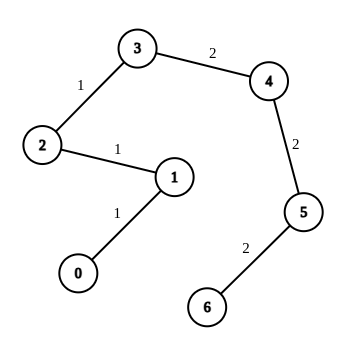
    输入：n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]

    输出：[0,0,1,3]

    解释：第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此，答案为 0 。

    第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 0 。

    第 3 条查询，将边 [2,3] 的权重变更为 2 。在这次操作之后，从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 1 。

    第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后，从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 3 。

    对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

    ```

    示例 2：

    ```txt

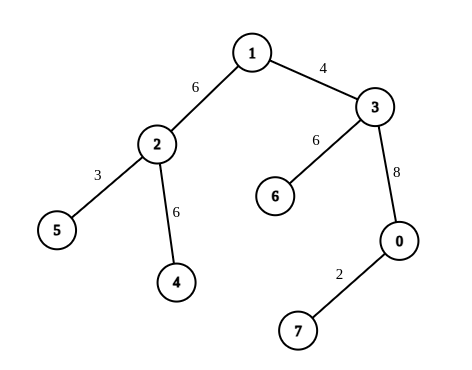
    输入：n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]

    输出：[1,2,2,3]

    解释：第 1 条查询，将边 [1,3] 的权重变更为 6 。在这次操作之后，从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此，答案为 1 。

    第 2 条查询，将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后，从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 2 。

    第 3 条查询，将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后，从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此，答案为 2 。

    第 4 条查询，将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后，从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 3 。

    对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

    ```

    提示：

    • 1 <= n <= 10^4

    • edges.length == n - 1

    • edges[i].length == 3

    • 0 <= ui, vi < n

    • 1 <= wi <= 26

    • 生成的输入满足 edges 表示一棵有效的树

    • 1 <= queries.length == m <= 2 * 10^4

    • queries[i].length == 2

    • 0 <= ai, bi < n

题目

2846. 边权重均等查询

现有一棵由 n 个节点组成的无向树，节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。

另给你一个长度为 m 的二维整数数组 queries ，其中 queries[i] = [ai, bi] 。对于每条查询，请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中，你可以选择树上的任意一条边，并将其权重更改为任意值。

注意：

  • 查询之间 相互独立 的，这意味着每条新的查询时，树都会回到 初始状态 。
  • 从 ai 到 bi的路径是一个由 不同 节点组成的序列，从节点 ai 开始，到节点 bi 结束，且序列中相邻的两个节点在树中共享一条边。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 条查询的答案。

示例 1：

1
2
3
4
5
6
7
输入：n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出：[0,0,1,3]
解释：第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此，答案为 0 。
第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 0 。
第 3 条查询，将边 [2,3] 的权重变更为 2 。在这次操作之后，从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 1 。
第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后，从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

示例 2：

1
2
3
4
5
6
7
输入：n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出：[1,2,2,3]
解释：第 1 条查询，将边 [1,3] 的权重变更为 6 。在这次操作之后，从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此，答案为 1 。
第 2 条查询，将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后，从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 3 条查询，将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后，从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 4 条查询，将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后，从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

提示：

  • 1 <= n <= 10^4
  • edges.length == n - 1
  • edges[i].length == 3
  • 0 <= ui, vi < n
  • 1 <= wi <= 26
  • 生成的输入满足 edges 表示一棵有效的树
  • 1 <= queries.length == m <= 2 * 10^4
  • queries[i].length == 2
  • 0 <= ai, bi < n

题解

方法一：

思路

这是个求lca的模板题。lca是最近公共祖先。

对于这个题，我们的思路是可以将这个树转化为有根树，然后每次查询求两个点的最近公共祖先。通过倍增法求最近公共祖先可以花费$O(nlogn)$时间预处理，后续每次查询两个点的最近公共祖先只需要$O(logn)$，在求最近公共祖先的同时，我们记录路径上所有不同边权出现的次数。然后我们只需要保留出现频次最高的边权x，其他的边权需要修改为x。边权种数不超过26种，查询次数为q次，查询花费的总时间是$26\times q \times log(n)$

我们注意到节点个数不超过10000，总操作次数应该没有超过1000万。这个时间复杂度是可以通过的。

下面介绍利用倍增法求lca。

预处理：st表是在线性结构上做倍增，类似于st表，我们可以在树状结构上倍增。依次处理每个节点第k个祖先，k是2的幂次。每个节点处理的次数不超过$log(n)$次。此外我们还需要记录每个节点x的深度d[x]。

查询lca：我们首先让查询的两个节点x和y处于同一深度。不妨设d[x] > d[y]。我们可以让x向上移动s = d[x]-d[y]条边，s可以看作是二进制数，则是由若干2的幂次组成。我们每次向上移动的边数恰好是2的幂次长度。所以不会超过$log(n)$次移动。当两个点处于同一深度，接下来我们将尝试两个点同时跳跃相同步数的边数。可以发现但跳跃到lca后他们会处于同一个节点。所以我们可以尝试各种2的幂次步数，只要没有处于同一个节点我们就同时跳跃。最后这两个点所处位置恰好是lca的子节点。

代码

这里两份代码，第一份超时，在以前我这种写法在比赛时是不会超时的。说明现在有大量测试用例没有达到最大数据范围。动态开辟空间反而减少了时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Solution {
public:
    #define N 10005
    vector<pair<int,int>> g[N];
    int fa[N][31], dep[N], cnt[N][31][27];

    // dfs，用来为 lca 算法做准备。接受两个参数：dfs 起始节点和它的父亲节点。
    void dfs(int u, int w, int fno) {
        // 初始化：第 2^0 = 1 个祖先就是它的父亲节点，dep 也比父亲节点多 1。
        fa[u][0] = fno;
        cnt[u][0][w]++;
        dep[u] = dep[fa[u][0]] + 1;
        // 初始化：其他的祖先节点：第 2^i 的祖先节点是第 2^(i-1) 的祖先节点的第
        // 2^(i-1) 的祖先节点。
        for (int i = 1; i < 31; ++i) {
            fa[u][i] = fa[fa[u][i - 1]][i - 1];
            for (int j=1; j<27; j++) {
                cnt[u][i][j] = cnt[u][i-1][j] + cnt[fa[u][i-1]][i-1][j];
            }
        }
        // 遍历子节点来进行 dfs。
        for (auto [v, e] : g[u]) {
            if (v == fno)
                continue;
            dfs(v, e, u);
        }
    }

    // lca。用倍增算法算取 x 和 y 的 lca 节点。
    int lca(int x, int y) {
        int len = dep[x] + dep[y];
        // 令 y 比 x 深。
        if (dep[x] > dep[y])
            swap(x, y);
        // 统计路径上每种权值的个数。
        vector<int> c(27);
        // 令 y 和 x 在一个深度。
        int tmp = dep[y] - dep[x];
        for (int j = 0; tmp; ++j, tmp >>= 1) if (tmp & 1) {
            for (int i=1; i<27; i++) {
                c[i] += cnt[y][j][i];
            }
            y = fa[y][j];
        }
        // 如果这个时候 y = x，那么 x，y 就都是它们自己的祖先。
        if (y == x) {
            return len - 2*dep[x] - *max_element(c.begin()+1, c.end());
        }
        // 不然的话，找到第一个不是它们祖先的两个点。
        for (int j = 30; j >= 0 && y != x; --j) {
            if (fa[x][j] != fa[y][j]) {
                for (int i=1; i<27; i++) {
                    c[i] += cnt[y][j][i] + cnt[x][j][i];
                }
                x = fa[x][j];
                y = fa[y][j];
            }
        }
        for (int i=1; i<27; i++) {
            c[i] += cnt[y][0][i] + cnt[x][0][i];
        }
        // 返回结果。
        return len - 2*dep[fa[x][0]] - *max_element(c.begin()+1, c.end());
    }

    void add(int x, int y, int val) {
        g[x].emplace_back(y, val);
        g[y].emplace_back(x, val);
    }
    vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
        for (auto& i:edges) {
            add(i[0]+1, i[1]+1, i[2]);
        }
        dfs(1, 0, 0);
        vector<int> ans;
        for (auto& i:queries) {
            ans.push_back(lca(i[0]+1, i[1]+1));
        }
        return ans;
    }
};

这份代码可以通过，我们在求lca的同时统计了路径上的不同权值的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
class Solution {
public:   
    vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
        vector<pair<int,int>> g[n+1];
        int fa[n+1][31], dep[n+1], cnt[n+1][31][27];
        memset(fa, 0, sizeof(fa));
        memset(dep, 0, sizeof(dep));
        memset(cnt, 0, sizeof(cnt));

        // dfs，用来为 lca 算法做准备。接受两个参数：dfs 起始节点和它的父亲节点。
        function<void(int,int,int)> dfs = [&](int u, int w, int fno) {
            // 初始化：第 2^0 = 1 个祖先就是它的父亲节点，dep 也比父亲节点多 1。
            fa[u][0] = fno;
            cnt[u][0][w]++;
            dep[u] = dep[fa[u][0]] + 1;
            // 初始化：其他的祖先节点：第 2^i 的祖先节点是第 2^(i-1) 的祖先节点的第
            // 2^(i-1) 的祖先节点。
            for (int i = 1; i < 31; ++i) {
                fa[u][i] = fa[fa[u][i - 1]][i - 1];
                for (int j=1; j<27; j++) {
                    cnt[u][i][j] = cnt[u][i-1][j] + cnt[fa[u][i-1]][i-1][j];
                }
            }
            // 遍历子节点来进行 dfs。
            for (auto [v, e] : g[u]) {
                if (v == fno)
                    continue;
                dfs(v, e, u);
            }
        };

        // lca。用倍增算法算取 x 和 y 的 lca 节点。
        auto lca = [&](int x, int y)->int {
            int len = dep[x] + dep[y];
            // 令 y 比 x 深。
            if (dep[x] > dep[y])
                swap(x, y);
            // 统计路径上每种权值的个数。
            vector<int> c(27);
            // 令 y 和 x 在一个深度。
            int tmp = dep[y] - dep[x];
            for (int j = 0; tmp; ++j, tmp >>= 1) if (tmp & 1) {
                for (int i=1; i<27; i++) {
                    c[i] += cnt[y][j][i];
                }
                y = fa[y][j];
            }
            // 如果这个时候 y = x，那么 x，y 就都是它们自己的祖先。
            if (y == x) {
                return len - 2*dep[x] - *max_element(c.begin()+1, c.end());
            }
            // 不然的话，找到第一个不是它们祖先的两个点。
            for (int j = 30; j >= 0 && y != x; --j) {
                if (fa[x][j] != fa[y][j]) {
                    for (int i=1; i<27; i++) {
                        c[i] += cnt[y][j][i] + cnt[x][j][i];
                    }
                    x = fa[x][j];
                    y = fa[y][j];
                }
            }
            for (int i=1; i<27; i++) {
                c[i] += cnt[y][0][i] + cnt[x][0][i];
            }
            // 返回结果。
            return len - 2*dep[fa[x][0]] - *max_element(c.begin()+1, c.end());
        };

        auto add = [&](int x, int y, int val) {
            g[x].emplace_back(y, val);
            g[y].emplace_back(x, val);
        };
        for (auto& i:edges) {
            add(i[0]+1, i[1]+1, i[2]);
        }
        dfs(1, 0, 0);
        vector<int> ans;
        for (auto& i:queries) {
            ans.push_back(lca(i[0]+1, i[1]+1));
        }
        return ans;
    }
};

这份代码也能通过，比上一份稍逊。因为我们是先求lca这个点，然后根据深度计算两个节点应该跳跃的步数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
class Solution {
public:   
    vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
        vector<pair<int,int>> g[n+1];
        int fa[n+1][31], dep[n+1], cnt[n+1][31][27];
        memset(fa, 0, sizeof(fa));
        memset(dep, 0, sizeof(dep));
        memset(cnt, 0, sizeof(cnt));

        // dfs，用来为 lca 算法做准备。接受两个参数：dfs 起始节点和它的父亲节点。
        function<void(int,int,int)> dfs = [&](int u, int w, int fno) {
            // 初始化：第 2^0 = 1 个祖先就是它的父亲节点，dep 也比父亲节点多 1。
            fa[u][0] = fno;
            cnt[u][0][w]++;
            dep[u] = dep[fa[u][0]] + 1;
            // 初始化：其他的祖先节点：第 2^i 的祖先节点是第 2^(i-1) 的祖先节点的第
            // 2^(i-1) 的祖先节点。
            for (int i = 1; i < 31; ++i) {
                fa[u][i] = fa[fa[u][i - 1]][i - 1];
                for (int j=1; j<27; j++) {
                    cnt[u][i][j] = cnt[u][i-1][j] + cnt[fa[u][i-1]][i-1][j];
                }
            }
            // 遍历子节点来进行 dfs。
            for (auto [v, e] : g[u]) {
                if (v == fno)
                    continue;
                dfs(v, e, u);
            }
        };

        // lca。用倍增算法算取 x 和 y 的 lca 节点。
        auto lca = [&](int x, int y)->int {
            int len = dep[x] + dep[y];
            // 令 y 比 x 深。
            if (dep[x] > dep[y])
                swap(x, y);
            // 令 y 和 x 在一个深度。
            int tmp = dep[y] - dep[x];
            for (int j = 0; tmp; ++j, tmp >>= 1) if (tmp & 1) {
                y = fa[y][j];
            }
            // 如果这个时候 y = x，那么 x，y 就都是它们自己的祖先。
            if (y == x) {
                return x;
            }
            // 不然的话，找到第一个不是它们祖先的两个点。
            for (int j = 30; j >= 0 && y != x; --j) {
                if (fa[x][j] != fa[y][j]) {
                    x = fa[x][j];
                    y = fa[y][j];
                }
            }
            // 返回结果。
            return fa[x][0];
        };

        auto add = [&](int x, int y, int val) {
            g[x].emplace_back(y, val);
            g[y].emplace_back(x, val);
        };
        for (auto& i:edges) {
            add(i[0]+1, i[1]+1, i[2]);
        }
        auto wcnt = [&](int x, int stp, vector<int>& c) {
            for (int j = 0; stp; ++j, stp >>= 1) if (stp & 1) {
                for (int i=1; i<27; i++) {
                    c[i] += cnt[x][j][i];
                }
                x = fa[x][j];
            }
        };
        dfs(1, 0, 0);
        vector<int> ans;
        for (auto& i:queries) {
            int x = i[0]+1, y = i[1]+1;
            int a = lca(x, y);
            // cout << a << endl;
            vector<int> c(27);
            wcnt(x, dep[x]-dep[a], c);
            wcnt(y, dep[y]-dep[a], c);
            ans.push_back(dep[x]+dep[y]-2*dep[a] - *max_element(c.begin()+1, c.end()));
        }
        return ans;
    }
};

方法二：

思路

我们还有一种求lca的rmq方法，先求树的欧拉序，并预处理出每个节点的深度。然后记录每个点x在欧拉序中的第一个位置p[x]。求两个点x和y的lca实际上就是欧拉序中的子区间[p[x], p[y]]中深度最小的点。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
class Solution {
public:   
    vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
        vector<pair<int,int>> g[n+1];
        vector<int> eulerTour, fc(n+1);
        int fa[n+1][31], dep[n+1], cnt[n+1][31][27];
        memset(fa, 0, sizeof(fa));
        memset(dep, 0, sizeof(dep));
        memset(cnt, 0, sizeof(cnt));

        auto add = [&](int x, int y, int val) {
            g[x].emplace_back(y, val);
            g[y].emplace_back(x, val);
        };
        for (auto& i:edges) {
            add(i[0]+1, i[1]+1, i[2]);
        }

        // dfs，用来为 lca 算法做准备。接受两个参数：dfs 起始节点和它的父亲节点。
        function<void(int,int,int)> dfs = [&](int u, int w, int fno) {
            // 初始化：第 2^0 = 1 个祖先就是它的父亲节点，dep 也比父亲节点多 1。
            fa[u][0] = fno;
            cnt[u][0][w]++;
            dep[u] = dep[fa[u][0]] + 1;

            // 每个节点欧拉序中第一次出现的位置
            fc[u] = eulerTour.size();
            eulerTour.push_back(u);
            
            // 初始化：其他的祖先节点：第 2^i 的祖先节点是第 2^(i-1) 的祖先节点的第
            // 2^(i-1) 的祖先节点。
            for (int i = 1; i < 31; ++i) {
                fa[u][i] = fa[fa[u][i - 1]][i - 1];
                for (int j=1; j<27; j++) {
                    cnt[u][i][j] = cnt[u][i-1][j] + cnt[fa[u][i-1]][i-1][j];
                }
            }
            // 遍历子节点来进行 dfs。
            for (auto [v, e] : g[u]) {
                if (v == fno)
                    continue;
                dfs(v, e, u);
                eulerTour.push_back(u);
            }
        };
        dfs(1, 0, 0);
    
        int st[eulerTour.size()][30]; //st[i][j] 代表区间[i, i+2^j)最小值

        auto ST = [&](const vector<int>& a) {
            int sz = a.size();
            for (int i=0; i<sz; i++) st[i][0] = a[i];
            for (int j=1; (1<<j)<=sz; j++) {//区间大小 
                for (int i=0; i+(1<<j)-1<sz; i++) {//区间下限 
                    int x = st[i][j-1], y = st[i+(1<<(j-1))][j-1];
                    st[i][j] = dep[x] < dep[y] ? x : y;
                }
            }
        };
        ST(eulerTour);

        auto ask = [&](int l, int r) {
            int k = 0;
            while ((1<<(k+1))<=r-l+1) k++;
            int x = st[l][k], y = st[r-(1<<k)+1][k];
            return  dep[x] < dep[y] ? x : y;
        };

        auto wcnt = [&](int x, int stp, vector<int>& c) {
            for (int j = 0; stp; ++j, stp >>= 1) if (stp & 1) {
                for (int i=1; i<27; i++) {
                    c[i] += cnt[x][j][i];
                }
                x = fa[x][j];
            }
        };
        vector<int> ans;
        for (auto& i:queries) {
            int x = i[0]+1, y = i[1]+1;
            int a = ask(min(fc[x], fc[y]), max(fc[x], fc[y]));
            vector<int> c(27);
            wcnt(x, dep[x]-dep[a], c);
            wcnt(y, dep[y]-dep[a], c);
            ans.push_back(dep[x]+dep[y]-2*dep[a] - *max_element(c.begin()+1, c.end()));
        }
        return ans;
    }
};