收集树中金币

题目

6356. 收集树中金币

---

给你一个 n 个节点的无向无根树，节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ，其中 coins[i] 可能为 0 也可能为 1 ，1 表示节点 i 处有一个金币。

一开始，你需要选择树中任意一个节点出发。你可以执行下述操作任意次：

• 收集距离当前节点距离为 2 以内的所有金币，或者
• 移动到树中一个相邻节点。

你需要收集树中所有的金币，并且回到出发节点，请你返回最少经过的边数。

如果你多次经过一条边，每一次经过都会给答案加一。

示例 1：

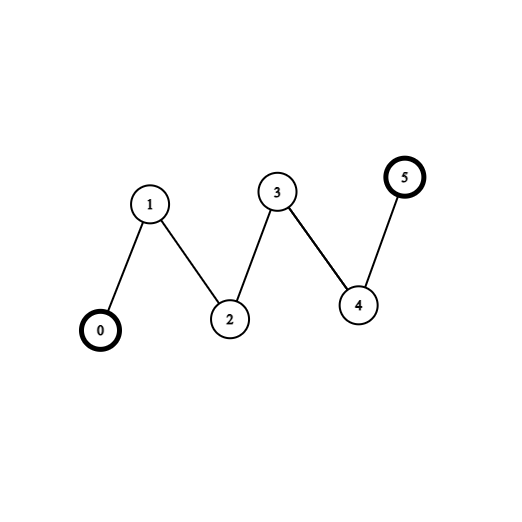
输入：coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：从节点 2 出发，收集节点 0 处的金币，移动到节点 3 ，收集节点 5 处的金币，然后移动回节点 2 。

示例 2：

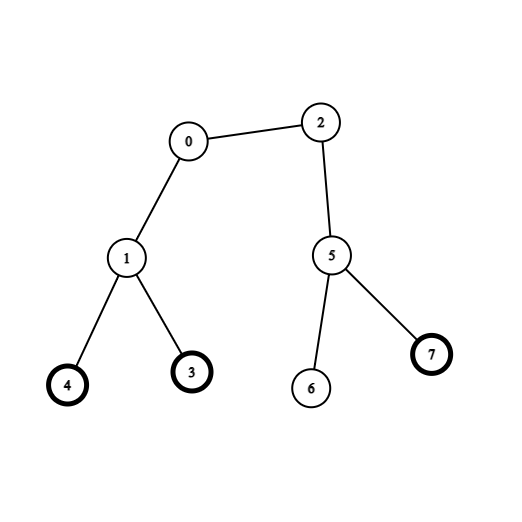
输入：coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
输出：2
解释：从节点 0 出发，收集节点 4 和 3 处的金币，移动到节点 2 处，收集节点 7 处的金币，移动回节点 0 。

提示：

• n == coins.length
• 1 <= n <= 3 * 10^4
• 0 <= coins[i] <= 1
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵合法的树。

题解

方法一：

思路

首先不断去除非金币叶子，这些节点无需访问，去除的方式就是拓扑排序。

剩余的叶子就都是金币，我们从这些节点再次拓扑排序，并记录每个节点的首次访问时间。

显然对于访问时间大于等于2的节点之间所连接的边我们需要访问两次。注意由于是树，所以没有环。

代码

class Solution {
public:
    int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {
        int n = coins.size();
        vector<int> deg(n);
        vector<vector<int>> g(n);
        for (auto& i:edges) {
            deg[i[0]]++;
            deg[i[1]]++;
            g[i[0]].push_back(i[1]);
            g[i[1]].push_back(i[0]);
        }
        queue<int> q;
        for (int i=0; i<n; i++) {
            if (deg[i] == 1 && coins[i] == 0) {
                q.push(i);
            }
        }
        // 拓扑排序 去除多余非金币叶子
        while (q.size()) {
            int u = q.front(); q.pop();
            for (int v:g[u]) {
                if (--deg[v] == 1 && coins[v] == 0) {
                    q.push(v);
                }
            }
        }
        // 叶子都为金币，记录每个节点的访问时间
        vector<int> vis(n);
        for (int i=0; i<n; i++) {
            if (deg[i] == 1 && coins[i] == 1) {
                q.push(i);
            }
        }
        while (q.size()) {
            int u = q.front(); q.pop();
            for (int v:g[u]) {
                if (--deg[v] == 1) {
                    vis[v] = vis[u] + 1;
                    q.push(v);
                }
            }
        }
        // for (int i:vis) cout << i << " ";
        // 统计边数
        int ans = 0;
        for (auto& i:edges) {
            if (vis[i[0]]>=2 && vis[i[1]]>=2) ans++;
        }
        return ans*2;
    }
};