圆形靶内的最大飞镖数量

题目

1453. 圆形靶内的最大飞镖数量

---

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。

投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r 。

请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。

示例 1：

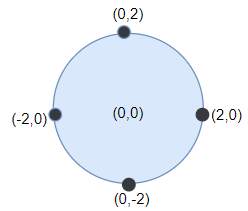
输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出：4
解释：如果圆形的飞镖靶的圆心为 (0,0) ，半径为 2 ，所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 4 。

示例 2：

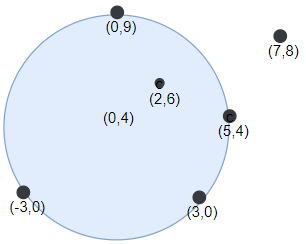
输入：points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出：5
解释：如果圆形的飞镖靶的圆心为 (0,4) ，半径为 5 ，则除了 (7,8) 之外的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 5 。

示例 3：

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
输出：1

示例 4：

输入：points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
输出：4

提示：

• 1 <= points.length <= 100
• points[i].length == 2
• -10^4 <= points[i][0], points[i][1] <= 10^4
• 1 <= r <= 5000

题解

方法一：

思路

枚举两个点在半径为r的圆上，求出圆心，然后统计每个点是否在圆内或圆上数目，维护一个最大值。时间复杂度O(n^3)

如何求圆心

设枚举的两个点为$A=(x_1, y_1), B=(x_2, y_2)$，两点的中点为$M = (\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$，圆心为$O=(x_0, y_0)$，$\vec{AM} = (\frac{x_2-x_1}{2}, \frac{y_2-y_1}{2})$，显然$\vec{AM} \cdot \vec{MO} = 0$，由此可以求出$\vec{MO} = (-\frac{y_2-y_1}{2}, \frac{2_2-2_1}{2}) \frac{|\vec{MO}|}{|\vec{AM}|}$，M已知可求出O

如何判断点没有在圆外

由于圆心可能是浮点数，如果点到圆心的距离大于半径，但是大的距离非常小可以认为是在点上。

代码

class Solution {
public:
    #define ll long long
    ll qdis(ll x1, ll y1, ll x2, ll y2) {
        return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
    }
    ll isle(double x, double y) {
        return x<=y || x>y&&x-y<=1e-9;
    }
    int numPoints(vector<vector<int>>& darts, int r) {
        int n = darts.size(), ans = 1;
        for (int i=0; i<n; i++) {
            for (int j=0; j<n; j++) {
                if (i == j) continue;
                ll x1 = darts[i][0], y1 = darts[i][1], x2 = darts[j][0], y2 = darts[j][1];
                if (qdis(x1, y1, x2, y2) > 4*r*r) continue;
                double x = (x2-x1)/2.0, y = (y2-y1)/2.0;
                double m = sqrt(x*x+y*y);
                double len = sqrt(r*r-x*x-y*y)/m;
                double x0 = x+x1-y*len, y0 = y+y1+x*len;
                // cout << x0 << " " << y0 << endl;
                int cnt = 0;
                for (auto& k:darts) {
                    if (isle((k[0]-x0)*(k[0]-x0) + (k[1]-y0)*(k[1]-y0), r*r)) cnt++;
                }
                ans = max(ans, cnt);
            }
        } 
        return ans;
    }
};