最小面积矩形 II

题目

963. 最小面积矩形 II

---

给定在 xy 平面上的一组点，确定由这些点组成的任何矩形的最小面积，其中矩形的边不一定平行于 x 轴和 y 轴。

如果没有任何矩形，就返回 0。

示例 1：

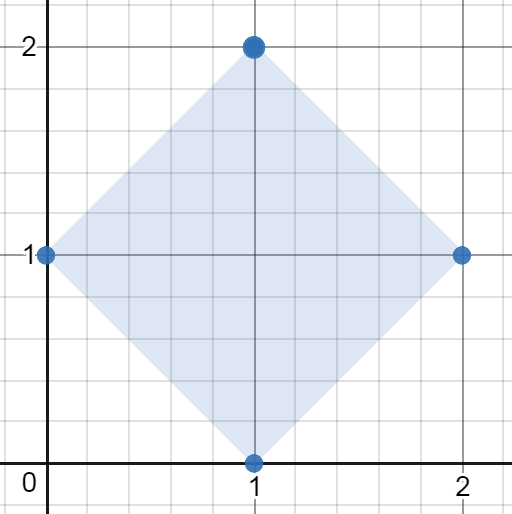
输入：[[1,2],[2,1],[1,0],[0,1]]
输出：2.00000
解释：最小面积的矩形出现在 [1,2],[2,1],[1,0],[0,1] 处，面积为 2。

示例 2：

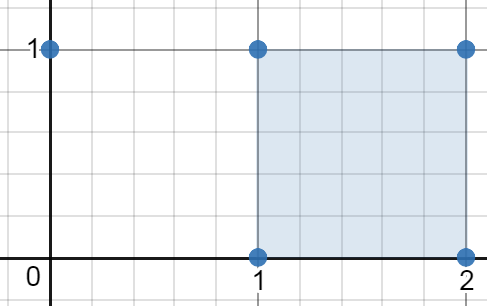
输入：[[0,1],[2,1],[1,1],[1,0],[2,0]]
输出：1.00000
解释：最小面积的矩形出现在 [1,0],[1,1],[2,1],[2,0] 处，面积为 1。

示例 3：

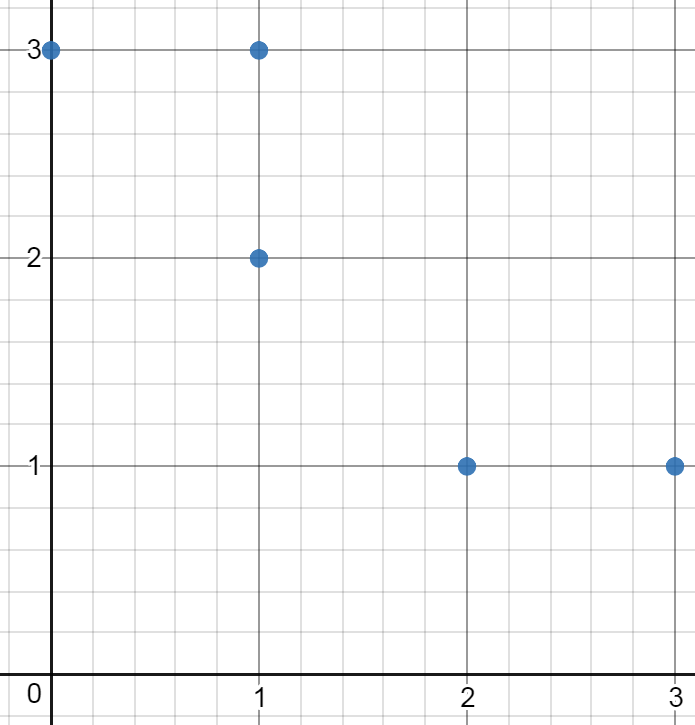
输入：[[0,3],[1,2],[3,1],[1,3],[2,1]]
输出：0
解释：没法从这些点中组成任何矩形。

示例 4：

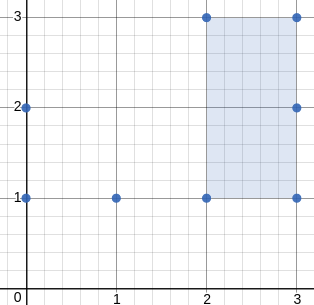
输入：[[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]
输出：2.00000
解释：最小面积的矩形出现在 [2,1],[2,3],[3,3],[3,1] 处，面积为 2。

提示：

1. 1 <= points.length <= 50
2. 0 <= points[i][0] <= 40000
3. 0 <= points[i][1] <= 40000
4. 所有的点都是不同的。
5. 与真实值误差不超过 10^-5 的答案将视为正确结果。

题解

方法一：

思路

枚举四个不同的点A,B,C,D，若相邻两个点的向量AB与另外两个点的向量CD平行且长度相等，若AB与AC垂直且AB与BD垂直 或者 AB与AD垂直且AB与BC垂直 则形成矩形。计算矩形面积。维护最小即可。时间复杂度$O(n^4)$

优化：

哈希表存储每个点，枚举三个不同点，是否形成直角三角形，再从哈希表中判断第四个点是否存在。时间复杂度$O(n^3)$

代码

class Solution {
public:
    using ll = long long;
    ll cross(ll x1, ll y1, ll x2, ll y2) {
        return x1*y2 - x2*y1;
    }
    ll mult(ll x1, ll y1, ll x2, ll y2) {
        return x1*x2 + y1*y2;
    }
    double minAreaFreeRect(vector<vector<int>>& points) {
        double ans = 1e15;
        int n = points.size();
        unordered_map<int,int> mp;
        for (auto& i:points) {
            mp[i[0]] = i[1];
        }
        for (int j=0; j<n; j++) {
            for (int i=0; i<n; i++) {
                for (int k=j+1; k<n; k++) {
                    if (i == j || i== k) continue;
                    auto& pj = points[j], &pi = points[i], &pk = points[k];
                    if (mult(pj[0]-pi[0], pj[1]-pi[1], pk[0]-pi[0], pk[1]-pi[1]) == 0 
                    && mp.count(pj[0]+pk[0]-pi[0]) && mp[pj[0]+pk[0]-pi[0]] == pj[1]+pk[1]-pi[1]) {
                        ans = min(ans, fabs(cross(pj[0]-pi[0], pj[1]-pi[1], pk[0]-pi[0], pk[1]-pi[1])));
                    }
                }
            }
        }
        if (1e15-ans < 1e-5) return 0;
        return ans;
    }
};