在网格图中访问一个格子的最少时间

题目

6366. 在网格图中访问一个格子的最少时间

---

给你一个 m x n 的矩阵 grid ，每个元素都为 非负 整数，其中 grid[row][col] 表示可以访问格子 (row, col) 的 最早 时间。也就是说当你访问格子 (row, col) 时，最少已经经过的时间为 grid[row][col] 。

你从 最左上角 出发，出发时刻为 0 ，你必须一直移动到上下左右相邻四个格子中的 任意 一个格子（即不能停留在格子上）。每次移动都需要花费 1 单位时间。

请你返回 最早 到达右下角格子的时间，如果你无法到达右下角的格子，请你返回 -1 。

示例 1：

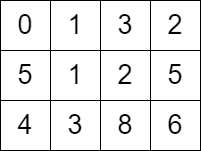
输入：grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
输出：7
解释：一条可行的路径为：
- 时刻 t = 0 ，我们在格子 (0,0) 。
- 时刻 t = 1 ，我们移动到格子 (0,1) ，可以移动的原因是 grid[0][1] <= 1 。
- 时刻 t = 2 ，我们移动到格子 (1,1) ，可以移动的原因是 grid[1][1] <= 2 。
- 时刻 t = 3 ，我们移动到格子 (1,2) ，可以移动的原因是 grid[1][2] <= 3 。
- 时刻 t = 4 ，我们移动到格子 (1,1) ，可以移动的原因是 grid[1][1] <= 4 。
- 时刻 t = 5 ，我们移动到格子 (1,2) ，可以移动的原因是 grid[1][2] <= 5 。
- 时刻 t = 6 ，我们移动到格子 (1,3) ，可以移动的原因是 grid[1][3] <= 6 。
- 时刻 t = 7 ，我们移动到格子 (2,3) ，可以移动的原因是 grid[2][3] <= 7 。
最终到达时刻为 7 。这是最早可以到达的时间。

示例 2：

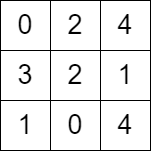
输入：grid = [[0,2,4],[3,2,1],[1,0,4]]
输出：-1
解释：没法从左上角按题目规定走到右下角。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 10^5
• 0 <= grid[i][j] <= 10^5
• grid[0][0] == 0

题解

方法一：

思路

最短路径问题

我们可以认为从一个格子走向另一个格子所花的时间不同。

如果走到当前格子最短的时间为t，需要前往的目标格子最早时间为x。

如果说t+1>=x则需要时间为1，否则由于不能一直待在同一个格子，所以需要在已走的格子间来回移动。

当再次来到当前格子时，所花的时间为t+2*k, k>=0。

所以满足t+2*k+1>=x才能移动，可求出最小的k=ceil((x-t-1)/2)

可以认为这是一个有权图，求最短路径即可。

代码

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    struct Node {
        int x,y;
        int s;
        bool operator<(const Node& o) const {
            return s > o.s;
        }
        Node(int x, int y, int s):x(x),y(y),s(s){}
    };
    int minimumTime(vector<vector<int>>& g) {
        if (g[0][1]>1 && g[1][0]>1) return -1;
        int n = g.size(), m = g[0].size();
        vector<vector<int>> stp(n, vector<int>(m, INF));
        stp[0][0] = 0;
        priority_queue<Node> q;
        q.emplace(0,0,0); 
        while (q.size()) {
            auto u = q.top(); q.pop();
            int x = u.x, y = u.y, s = u.s;
            for (int i=0; i<4; i++) {
                int mx = x+(i-1)%2;
                int my = y+(i-2)%2;
                if (mx<0 || mx>=n || my<0 || my>=m) continue;
                int k = max(0, (g[mx][my]-stp[x][y])/2);
                if (stp[mx][my] > stp[x][y]+k*2+1) {
                    stp[mx][my] = stp[x][y]+k*2+1;
                    q.emplace(mx, my, stp[mx][my]);
                }
            }
        }
        return stp[n-1][m-1] == INF ? -1 : stp[n-1][m-1];
    }
};