设计可以求最短路径的图类

发表于 2023-04-16 更新于 2024-06-07 分类于 leetcode

给你一个有 n 个节点的 有向带权 图，节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示，其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。

请你实现一个 Graph 类：

Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
addEdge(int[] edge) 向边集中添加一条边，其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径最小代价。如果路径不存在，返回 -1 。一条路径的代价是路径中所有边代价之和。

示例 1：

```txt

输入：

["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]

[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]

输出：

[null, 6, -1, null, 6]

解释：

Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);

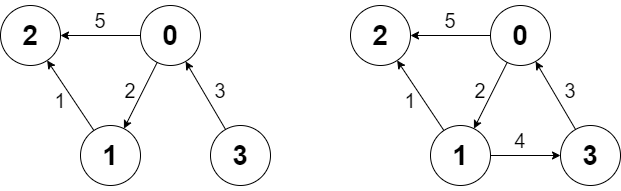
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示：3 -> 0 -> 1 -> 2 ，总代价为 3 + 2 + 1 = 6 。

g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。

g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边，得到第二幅图。

g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ，总代价为 2 + 4 = 6 。

```

提示：

1 <= n <= 100
0 <= edges.length <= n * (n - 1)
edges[i].length == edge.length == 3
0 <= fromi, toi, from, to, node1, node2 <= n - 1
1 <= edgeCosti, edgeCost <= 10^6
图中任何时候都不会有重边和自环。
调用 addEdge 至多 100 次。
调用 shortestPath 至多 100 次。

题目

6336. 设计可以求最短路径的图类

请你实现一个 Graph 类：

Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
addEdge(int[] edge) 向边集中添加一条边，其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径最小代价。如果路径不存在，返回 -1 。一条路径的代价是路径中所有边代价之和。

示例 1：

输入：
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
输出：
[null, 6, -1, null, 6]

解释：
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示：3 -> 0 -> 1 -> 2 ，总代价为 3 + 2 + 1 = 6 。
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边，得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ，总代价为 2 + 4 = 6 。

提示：

1 <= n <= 100
0 <= edges.length <= n * (n - 1)
edges[i].length == edge.length == 3
0 <= fromi, toi, from, to, node1, node2 <= n - 1
1 <= edgeCosti, edgeCost <= 10^6
图中任何时候都不会有重边和自环。
调用 addEdge 至多 100 次。
调用 shortestPath 至多 100 次。

题解

方法一：

思路

Floyd算法，$O(n^3)$的时间复杂度求多源最短路径。

其思想是动态规划。
设图中共n个节点，节点编号从0到n-1。
定义f[k][x][y]，表示只允许经过节点 0 到 k-1，节点 x 到节点 y 的最短路长度。

初始化f[0][][]：

若节点u和v之间存在边权为e的有向边，则f[0][u][v] = e
对角线初始化为0，f[0][i][i] = 0
其余初始化为无穷，f[0][i][j] = INF, i != j

状态转移

f[k][x][y] = min(f[k-1][x][y], f[k-1][x][k]+f[k-1][k][y]) 经过k的最短路径和不经过k的最短路径选择最小的一条。

本题图中点数不超100，边数也不会超过10000，我们跑一次Floyd大概需要1e6的操作数。
但是后续会有不超过100次的添加边操作。如果每添加一条边都跑一次Floyd那么势必超时。

有什么优化的地方呢？
注意到新增加的边可以让某两个节点x与y的最短距离变小，说明x到y的路径上一定经过了新增的这条边。
所以我们只需花$O(n^2)$跟新任意两个点的最短距离即可。

设e1到e2新增的有向边，边权为e3。

则有
f[k][e1][e2] = min(f[k][e1][e2], e3),
f[k][x][y] = min(f[k][x][y], f[k][x][e1]+f[k][e1][e2]+f[k][e2][y])

注意到每次转移f[i+1][][]只与f[i][][]有关，所以可以将数组减少一维。

代码

class Graph {
public:
    int INF = 0x3f3f3f3f;
    int f[105][105];
    int n;
    Graph(int n, vector<vector<int>>& edges):n(n) {
        memset(f, 0x3f, sizeof(f));
        for (int i=0; i<n; i++) f[i][i] = 0;
        
        for (auto& i:edges) {
            f[i[0]][i[1]] = i[2];
        }
        for (int k=0; k<n; k++) {
            for (int i=0; i<n; i++) {
                for (int j=0; j<n; j++) {
                    f[i][j] = min(f[i][j], f[i][k]+f[k][j]);
                }
            }
        }
    }
    
    void addEdge(vector<int> e) {
        f[e[0]][e[1]] = min(f[e[0]][e[1]], e[2]);
        for (int i=0; i<n; i++) {
            for (int j=0; j<n; j++) {
                f[i][j] = min(f[i][j], f[i][e[0]]+f[e[0]][e[1]]+f[e[1]][j]);
            }
        }
    }
    
    int shortestPath(int node1, int node2) {
        return (f[node1][node2]+1)%(INF+1)-1;
    }
};

/**
 * Your Graph object will be instantiated and called as such:
 * Graph* obj = new Graph(n, edges);
 * obj->addEdge(edge);
 * int param_2 = obj->shortestPath(node1,node2);
 */

方法二：

思路

每加一条边做一次dijkstra。
由于是稠密图用暴力的dijkstra时间复杂度为$O(n^2)$。n为图中点数。

优先队列优化的时间复杂度为$O(mlog(m))$，m为图中边数。由于稠密图最多能达到n*(n-1)条边。
所以时间复杂度最坏能达到$O(n^2logn^2)$

本题n不超过100，使用暴力的操作数数量级1e6，优先队列应该最多是1e7，所以优先队列优化应该也能过。

代码

暴力dijkstra

class Graph {
public:
    int INF = 0x3f3f3f3f;
    int f[105][105];
    int maxn;
    Graph(int n, vector<vector<int>>& edges):maxn(n) {
        memset(f, 0x3f, sizeof(f));
        for (int i=0; i<n; i++) f[i][i] = 0;

        for (auto& i:edges) {
            f[i[0]][i[1]] = i[2];
        }

    }
    
    void addEdge(vector<int> e) {
        f[e[0]][e[1]] = e[2];
    }
    
    int shortestPath(int node1, int node2) {
        int dis[maxn], vis[maxn];
        memset(dis, 0x3f, sizeof(dis));
        memset(vis, 0, sizeof(vis));
        dis[node1] = 0;
        for (int i = 0; i < maxn; i++) {
            int u = 0, mind = INF;
            for (int j = 0; j < maxn; j++)
                if (!vis[j] && dis[j] < mind)
                    u = j, mind = dis[j];
            vis[u] = true;
            for (int v = 0; v < maxn; v++) {
                int w = f[u][v];
                if (dis[v] > dis[u] + w)
                    dis[v] = dis[u] + w;
            }
        }
        return (dis[node2]+1)%(INF+1)-1;
    }
};

/**
 * Your Graph object will be instantiated and called as such:
 * Graph* obj = new Graph(n, edges);
 * obj->addEdge(edge);
 * int param_2 = obj->shortestPath(node1,node2);
 */

优先队列优化dijkstra

class Graph {
public:
    const int INF = 0x3f3f3f3f;
    vector<vector<pair<int,int>>> g;
    int n;
    Graph(int n, vector<vector<int>>& edges): g(n), n(n){
        for (auto& i:edges) {
            g[i[0]].emplace_back(i[1], i[2]);
        }
    }
    
    void addEdge(vector<int> e) {
        g[e[0]].emplace_back(e[1], e[2]);
    }
    
    int shortestPath(int node1, int node2) {
        vector<int> dis(n, INF), vis(n, 0);
        dis[node1] = 0;
        priority_queue<pair<int,int>> q;
        q.emplace(0, node1);
        while (q.size()) {
            auto [d, u] = q.top(); q.pop();
            if (vis[u]) continue;
            vis[u] = 1;
            for (auto [i,e]:g[u]) {
                if (dis[i] > dis[u]+e) {
                    dis[i] = dis[u]+e;
                    q.emplace(-dis[i], i);
                } 
            }
        }
        return dis[node2]==INF?-1:dis[node2];
        
    }
};

/**
 * Your Graph object will be instantiated and called as such:
 * Graph* obj = new Graph(n, edges);
 * obj->addEdge(edge);
 * int param_2 = obj->shortestPath(node1,node2);
 */