物块放置查询

发表于 分类于

    物块放置查询

    有一条无限长的数轴，原点在 0 处，沿着 x 轴 正 方向无限延伸。

    给你一个二维数组 queries ，它包含两种操作：

    1. 操作类型 1 ：queries[i] = [1, x] 。在距离原点 x 处建一个障碍物。数据保证当操作执行的时候，位置 x 处 没有 任何障碍物。

    2. 操作类型 2 ：queries[i] = [2, x, sz] 。判断在数轴范围 [0, x] 内是否可以放置一个长度为 sz 的物块，这个物块需要 完全 放置在范围 [0, x] 内。如果物块与任何障碍物有重合，那么这个物块 不能 被放置，但物块可以与障碍物刚好接触。注意，你只是进行查询，并 不是 真的放置这个物块。每个查询都是相互独立的。

    请你返回一个 boolean 数组results ，如果第 i 个操作类型 2 的操作你可以放置物块，那么 results[i] 为

    true ，否则为 false 。

    示例 1：

    输入： queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]

    输出：[false,true,true]

    解释：

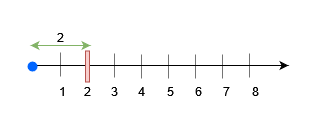
    查询 0 ，在 x = 2 处放置一个障碍物。在 x = 3 之前任何大小不超过 2 的物块都可以被放置。

    示例 2：

    输入： queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]

    输出：[true,true,false]

    解释：

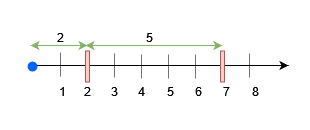
    • 查询 0 在 x = 7 处放置一个障碍物。在 x = 7 之前任何大小不超过 7 的物块都可以被放置。

    • 查询 2 在 x = 2 处放置一个障碍物。现在，在 x = 7 之前任何大小不超过 5 的物块可以被放置，x = 2 之前任何大小不超过 2 的物块可以被放置。

    提示：

    • 1 <= queries.length <= 15 * 104

    • 2 <= queries[i].length <= 3

    • 1 <= queries[i][0] <= 2

    • 1 <= x, sz <= min(5 * 104, 3 * queries.length)

    • 输入保证操作 1 中，x 处不会有障碍物。

    • 输入保证至少有一个操作类型 2 。

题目

物块放置查询

有一条无限长的数轴，原点在 0 处，沿着 x 轴 正 方向无限延伸。

给你一个二维数组 queries ，它包含两种操作：

  1. 操作类型 1 ：queries[i] = [1, x] 。在距离原点 x 处建一个障碍物。数据保证当操作执行的时候，位置 x 处 没有 任何障碍物。
  2. 操作类型 2 ：queries[i] = [2, x, sz] 。判断在数轴范围 [0, x] 内是否可以放置一个长度为 sz 的物块，这个物块需要 完全 放置在范围 [0, x] 内。如果物块与任何障碍物有重合，那么这个物块 不能 被放置，但物块可以与障碍物刚好接触。注意，你只是进行查询，并 不是 真的放置这个物块。每个查询都是相互独立的。

请你返回一个 boolean 数组results ，如果第 i 个操作类型 2 的操作你可以放置物块，那么 results[i] 为
true ，否则为 false 。

示例 1：

输入： queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]

输出：[false,true,true]

解释：

查询 0 ，在 x = 2 处放置一个障碍物。在 x = 3 之前任何大小不超过 2 的物块都可以被放置。

示例 2：

输入： queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]

输出：[true,true,false]

解释：

  • 查询 0 在 x = 7 处放置一个障碍物。在 x = 7 之前任何大小不超过 7 的物块都可以被放置。
  • 查询 2 在 x = 2 处放置一个障碍物。现在，在 x = 7 之前任何大小不超过 5 的物块可以被放置，x = 2 之前任何大小不超过 2 的物块可以被放置。

提示：

  • 1 <= queries.length <= 15 * 104
  • 2 <= queries[i].length <= 3
  • 1 <= queries[i][0] <= 2
  • 1 <= x, sz <= min(5 * 104, 3 * queries.length)
  • 输入保证操作 1 中，x 处不会有障碍物。
  • 输入保证至少有一个操作类型 2 。

题解

方法一:

思路

线段树维护每个区间的最大连续非障碍长度mx。涉及单点修改，区间内查询最大连续非障碍长度。

两个区间的最大连续非障碍长度，不能直接合并。还需要记录每个区间最左端的障碍位置lb和最右端的障碍位置rb。

两个子区间合并成当前区间的情况，少许复杂。

  • 对于左右子区间都存在障碍的情况下，当前区间的mx是左右区间的mx，以及右区间lb-左区间rb，三者的最值。
  • 对于左子区间存在障碍且右子区间不存在障碍的情况下，当前区间的mx是左区间的mx，以及右区间右端点-左区间rb，二者的最值。
  • 对于左子区间不存在障碍且右子区间存在障碍的情况下，当前区间的mx是右区间的mx，以及右区间lb-左区间左端点，二者的最值。
  • 对于左右子区间都不存在障碍的情况下，当前区间的mx是两个区间长度的和。

当前区间的lb,rb同理分析即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#define ls (id<<1)
#define rs (id<<1|1)
template<class t,class u> ostream& operator<<(ostream& os,const pair<t,u>& p) {
    return os<<'['<<p.first<<", "<<p.second<<']';
}
template<class t> ostream& operator<<(ostream& os,const vector<t>& v) {
    os<<'['; int s = 1;
    for(auto e:v) { if (s) s = 0; else os << ", "; os << e; }
    return os<<']';
}
template<class t,class u> ostream& operator<<(ostream& os,const map<t,u>& mp){
    os<<'{'; int s = 1;
    for(auto [x,y]:mp) { if (s) s = 0; else os << ", "; os<<x<<": "<<y; }
    return os<<'}';
}
struct Node {
    int mx, lb, rb;
    Node(int mx, int lb, int rb):mx(mx), lb(lb), rb(rb) {}
};
ostream& operator<<(ostream& os,const Node& p) {
    return os<<'['<<p.lb<<", "<<p.rb<<", "<<p.mx<<']';
}
class Solution {
public:
    
    const int NA = -2;
    vector<bool> getResults(vector<vector<int>>& queries) {
        int hsz = queries.size()*3+5;
        int sz = 4*(hsz);
        vector<int> mx(sz, 0), lb(sz, NA), rb(sz, NA);
        function<void(int,int,int)> build = [&](int id, int l, int r) {
            mx[id] = r-l;
            if (l==r) {
                
                return ;
            }
            int m = l+r>>1;
            build(ls, l, m);
            build(rs, m+1, r);

        };
        build(1, 0, hsz);
        function<void(int,int,int,int)> add = [&](int id, int l, int r, int q) {
            if (l == r) {
                mx[id] = 0;
                lb[id] = rb[id] = l;
                return ;
            }
            int m = l+r>>1; 
            if (q <= m)
                add(ls, l, m, q);
            else
                add(rs, m+1, r, q);
            if (lb[ls] != NA && lb[rs] != NA) {
                mx[id] = max({mx[ls], mx[rs], lb[rs]-rb[ls]});
                lb[id] = lb[ls];
                rb[id] = rb[rs];
            } else if (lb[ls] != NA) {
                mx[id] = max(mx[ls], r-rb[ls]);
                lb[id] = lb[ls];
                rb[id] = rb[ls];
            } else if (lb[rs] != NA) {
                mx[id] = max(mx[rs], lb[rs]-l);
                lb[id] = lb[rs];
                rb[id] = rb[rs];
            } else {
                mx[id] = r-l;
            }
        };
        auto push_up = [&](Node a, Node b, int l, int r) {
            Node rt(0,NA, NA);
            if (a.lb != NA && b.lb != NA) {
                rt.mx = max({a.mx, b.mx, b.lb-a.rb});
                rt.lb = a.lb;
                rt.rb = b.rb;
            } else if (a.lb != NA) {
                rt.mx = max(a.mx, r-a.rb);
                rt.lb = a.lb;
                rt.rb = a.rb;
            } else if (b.lb != NA) {
                rt.mx = max(b.mx, b.lb-l);
                rt.lb = b.lb;
                rt.rb = b.rb;
            } else {
                rt.mx = r-l;
            }
            return rt;
        };
        function<Node(int,int,int,int,int)> ask = [&](int id, int l, int r, int ql, int qr) {
            if (ql <= l && r <= qr) { 
                return Node(mx[id], lb[id], rb[id]);
            }
            int m = l + r >> 1;
            if (qr<=m) {
                return ask(ls, l, m, ql, qr);
            } else if (m<ql) {
                return ask(rs, m+1, r, ql, qr);
            } else {
                // cout << l << " -- " << r << endl;
                Node rt = push_up(ask(ls, l, m, ql, qr), ask(rs, m+1, r, ql, qr), max(l, ql), min(r, qr));
                // cout << rt << endl;
                return rt;
            }
        };
        // cout << "-1\n" << endl;
        vector<bool> ans;
        for (auto& i:queries) {
            // cout << i << endl;
            int o = i[0];
            if (o == 1) {
                add(1, 0, hsz, i[1]);
            } else {
                Node rt = ask(1, 0, hsz, 0, i[1]);
                // cout << rt.lb << " - " << rt.rb << " " << rt.mx << endl;
                ans.push_back(rt.mx >= i[2]);
            }
        }
        return ans;
    }
};