2290. 到达角落需要移除障碍物的最小数目
给你一个下标从 0 开始的二维整数数组 grid ,数组大小为 m x n 。每个单元格都是两个值之一:
0 表示一个 空 单元格,
1 表示一个可以移除的 障碍物 。
你可以向上、下、左、右移动,从一个空单元格移动到另一个空单元格。
现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ,返回需要移除的障碍物的 最小 数目。
示例 1:
```txt
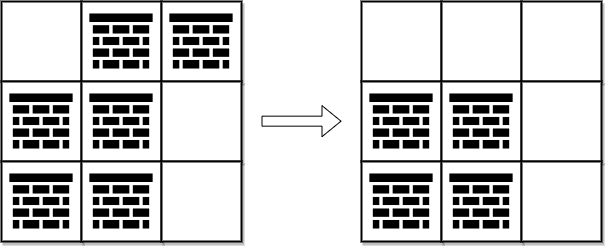
输入:grid = [[0,1,1],[1,1,0],[1,1,0]]
输出:2
解释:可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。
可以证明我们至少需要移除两个障碍物,所以返回 2 。
注意,可能存在其他方式来移除 2 个障碍物,创建出可行的路径。
```
示例 2:
```txt
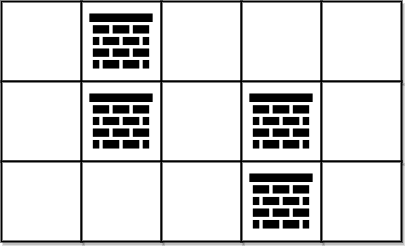
输入:grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
输出:0
解释:不移除任何障碍物就能从 (0, 0) 到 (2, 4) ,所以返回 0 。
```
提示:
">
题目
2290. 到达角落需要移除障碍物的最小数目
给你一个下标从 0 开始的二维整数数组 grid ,数组大小为 m x n 。每个单元格都是两个值之一:
-
0 表示一个 空 单元格,
-
1 表示一个可以移除的 障碍物 。
你可以向上、下、左、右移动,从一个空单元格移动到另一个空单元格。
现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ,返回需要移除的障碍物的 最小 数目。
示例 1:
![]()
1
2
3
4
5
| 输入:grid = [[0,1,1],[1,1,0],[1,1,0]]
输出:2
解释:可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。
可以证明我们至少需要移除两个障碍物,所以返回 2 。
注意,可能存在其他方式来移除 2 个障碍物,创建出可行的路径。
|
示例 2:
![]()
1
2
3
| 输入:grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
输出:0
解释:不移除任何障碍物就能从 (0, 0) 到 (2, 4) ,所以返回 0 。
|
提示:
-
m == grid.length
-
n == grid[i].length
-
1 <= m, n <= 10^5
-
2 <= m * n <= 10^5
-
grid[i][j] 为 0 或 1
grid[0][0] == grid[m - 1][n - 1] == 0
题解
方法一:
思路
建图
对于从当前点走向障碍物,则建立一条边权为1的边。
对于从当前点走向空单元格,则建立一条边权为0的边。
然后求最短路径即可。
可用01dfs或dijkstra。
代码
01bfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
const int INF = 0x3f3f3f3f;
int minimumObstacles(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
deque<pair<int,int>> que;
que.emplace_back(0,0);
int dis[n][m];
memset(dis, 0x3f, sizeof(dis));
dis[0][0] = 0;
while (!que.empty()) {
auto [x, y] = que.front(); que.pop_front();
for (int i=0; i<4; i++) {
int mx = (i-1)%2+x;
int my = (i-2)%2+y;
if (mx<0 || mx>=n || my<0 || my>=m) continue;
int val = grid[mx][my] == 1 ? 1 : 0;
if (dis[mx][my] > dis[x][y]+val) {
dis[mx][my] = dis[x][y]+val;
if (val) que.emplace_back(mx, my);
else que.emplace_front(mx, my);
}
}
}
return dis[n-1][m-1];
}
};
|
dijkstra
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
public:
struct Node {
int x, y;
int dis;
bool operator<(const Node& o) const {
return dis > o.dis;
}
};
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};
int minimumObstacles(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
int INF = 0x3f3f3f3f;
priority_queue<Node> que;
vector<vector<int>> dis(n, vector<int>(m, INF));
que.push({0,0,0});
dis[0][0] = 0;
while (!que.empty()) {
auto node = que.top(); que.pop();
int x = node.x;
int y = node.y;
int d = node.dis;
for (int i=0; i<4; i++) {
int mx = dx[i]+x;
int my = dy[i]+y;
if (mx<0 || mx>=n || my<0 || my>=m) continue;
int val = grid[mx][my] == 1 ? 1 : 0;
if (dis[mx][my] > dis[x][y]+val) {
dis[mx][my] = dis[x][y]+val;
que.push({mx,my,dis[mx][my]});
}
}
}
return dis[n-1][m-1];
}
};
|



