1263. 推箱子
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m x n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
玩家用字符 'S' 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
地板用字符 '.' 表示,意味着可以自由行走。
墙用字符 '#' 表示,意味着障碍物,不能通行。
箱子仅有一个,用字符 'B' 表示。相应地,网格上有一个目标位置 'T'。
玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
示例 1:
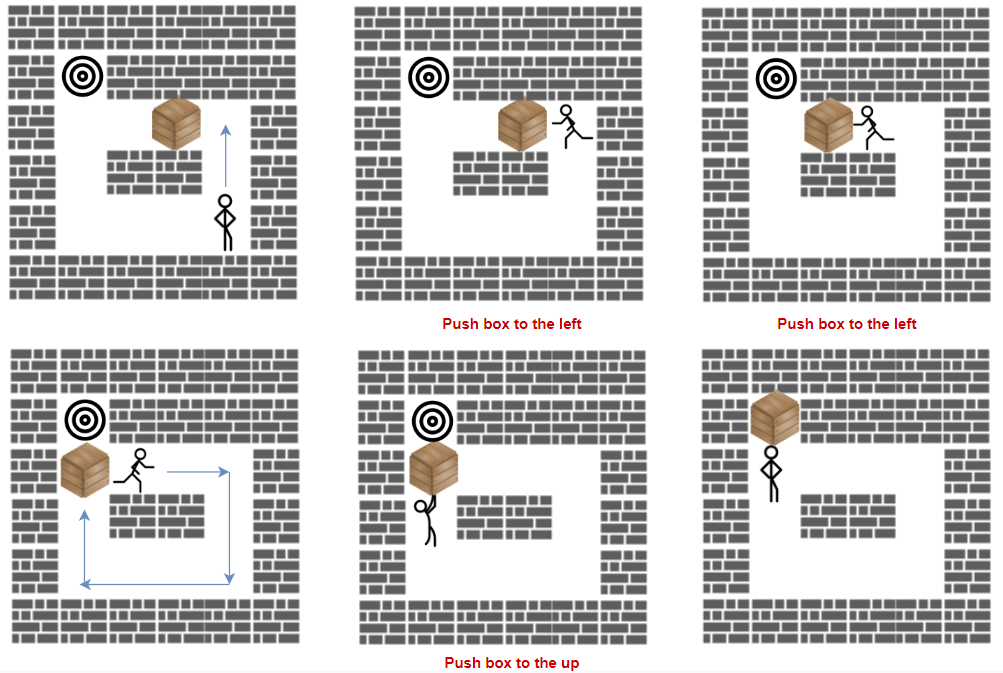
```txt
输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:3
解释:我们只需要返回推箱子的次数。
```
示例 2:
```txt
输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:-1
```
示例 3:
```txt
输入:grid = [["#","#","#","#","#","#"],
["#","T",".",".","#","#"],
["#",".","#","B",".","#"],
["#",".",".",".",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:5
解释:向下、向左、向左、向上再向上。
```
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 20
grid 仅包含字符 '.', '#', 'S' , 'T', 以及 'B'。
grid 中 'S', 'B' 和 'T' 各只能出现一个。
">
题目
1263. 推箱子
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m x n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
- 玩家用字符
'S' 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
- 地板用字符
'.' 表示,意味着可以自由行走。
- 墙用字符
'#' 表示,意味着障碍物,不能通行。
- 箱子仅有一个,用字符
'B' 表示。相应地,网格上有一个目标位置 'T'。
- 玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
- 玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
示例 1:
![]()
1
2
3
4
5
6
7
8
| 输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:3
解释:我们只需要返回推箱子的次数。
|
示例 2:
1
2
3
4
5
6
7
| 输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:-1
|
示例 3:
1
2
3
4
5
6
7
8
| 输入:grid = [["#","#","#","#","#","#"],
["#","T",".",".","#","#"],
["#",".","#","B",".","#"],
["#",".",".",".",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:5
解释:向下、向左、向左、向上再向上。
|
提示:
-
m == grid.length
-
n == grid[i].length
-
1 <= m, n <= 20
-
grid 仅包含字符 '.', '#', 'S' , 'T', 以及 'B'。
grid 中 'S', 'B' 和 'T' 各只能出现一个。
题解
方法一:
思路
我们需要箱子到目标点的最小距离,箱子的移动方向有四种但是有些位置的移动方向不可用。
我们注意到每次箱子移动完后,人的位置就代替了之前的箱子的位置。
那么我们可以用状态$f_{x,y,z}$代表箱子在坐标(x,y)位置且人在坐标(x+(z-1)%2, y+(z-2)%2)的最小移动次数。
(z取值在0到3,这样人的位置就有4种(x-1,y), (x,y-1), (x+1,y), (x,y+1))
状态的转移可以用BFS来完成。
我们需要先找到初始状态,也就是人一开始可以在箱子四周的位置个数。然后加入队列。
在队列中每次出队一个状态,我们考虑可以转移到哪些状态:
若出队$f_{i,j,z}$,能转移的状态为$f_{i’,j’,z’}$,则$(i’,j’)$是$(i,j)$的四周的一个位置且不能越界,不能为墙。然后$z$和$z’$在不经过$(i,j)$必须连通。
数据范围n最多20,m最多20。
总状态数4nm个,每次状态转移方向有4个,每个需要用BFS花$O(nm)$时间来检测连通性。
时间复杂度为$O(n^2m^2)$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
| class Solution {
public:
const int INF = 0x3f3f3f3f;
int minPushBox(vector<vector<char>>& g) {
int n = g.size(), m = g[0].size();
int box_x, box_y, peo_x, peo_y, tar_x, tar_y;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (g[i][j] == 'S') {
peo_x = i, peo_y = j, g[i][j] = '.';
}
if (g[i][j] == 'B') {
box_x = i, box_y = j, g[i][j] = '.';
}
if (g[i][j] == 'T') {
tar_x = i, tar_y = j, g[i][j] = '.';
}
}
}
auto check = [&](int x, int y, int p1, int p2) {
int sx = x+(p1-1)%2, sy = y+(p1-2)%2;
int tx = x+(p2-1)%2, ty = y+(p2-2)%2;
if (sx<0 || sx>=n || sy<0 || sy>=m || g[sx][sy] != '.') return false;
if (tx<0 || tx>=n || ty<0 || ty>=m || g[tx][ty] != '.') return false;
vector<vector<int>> vis(n, vector<int>(m,0));
vis[sx][sy] = 1;
queue<pair<int,int>> q;
q.emplace(sx, sy);
while (q.size()) {
auto [a, b] = q.front(); q.pop();
if (a == tx && b == ty) {
return true;
}
for (int i=0; i<4; i++) {
int ma = a+(i-1)%2, mb = b+(i-2)%2;
if (ma<0 || ma>=n || mb<0 || mb>=m || ma==x && mb==y ||
g[ma][mb]=='#' || vis[ma][mb])
continue;
vis[ma][mb] = 1;
q.emplace(ma, mb);
}
}
return false;
};
auto get_start = [&]() {
vector<vector<int>> dis(n, vector<int>(m, INF));
dis[peo_x][peo_y] = 0;
queue<pair<int,int>> q;
q.emplace(peo_x, peo_y);
while (q.size()) {
auto [x, y] = q.front(); q.pop();
for (int i=0; i<4; i++) {
int mx = x+(i-1)%2;
int my = y+(i-2)%2;
if (mx<0 || mx>=n || my<0 || my>=m ||
mx == box_x && my == box_y || g[mx][my] == '#' || dis[mx][my] != INF)
continue;
dis[mx][my] = dis[x][y] + 1;
q.emplace(mx, my);
}
}
vector<tuple<int,int,int>> rt;
for (int i=0; i<4; i++) {
int mx = box_x+(i-1)%2;
int my = box_y+(i-2)%2;
if (mx<0 || mx>=n || my<0 || my>=m || g[mx][my] == '#' || dis[mx][my] == INF)
continue;
rt.emplace_back(box_x, box_y, i);
}
return rt;
};
queue<tuple<int,int,int>> q;
int vis[22][22][5];
memset(vis, 0, sizeof(vis));
auto s = get_start();
for (auto [i,j,k]: s) {
q.emplace(i,j,k);
vis[i][j][k] = 1;
}
int stp = 0;
while (q.size()) {
int sz = q.size();
for (int _=0; _<sz; _++) {
auto [x, y, z] = q.front(); q.pop();
if (x == tar_x && y == tar_y) return stp;
for (int i=0; i<4; i++) {
int mx = x+(i-1)%2;
int my = y+(i-2)%2;
if (!check(x,y,z,(i+2)%4) || mx<0 || mx>=n || my<0 || my>=m
|| g[mx][my] == '#'|| vis[mx][my][(i+2)%4])
continue;
vis[mx][my][(i+2)%4] = 1;
q.emplace(mx,my,(i+2)%4);
}
}
stp++;
}
return -1;
}
};
|

