网格图中最少访问的格子数

题目

6353. 网格图中最少访问的格子数

---

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。

当你在格子 (i, j) 的时候，你可以移动到以下格子之一：

• 满足 j < k <= grid[i][j] + j 的格子 (i, k) （向右移动），或者
• 满足 i < k <= grid[i][j] + i 的格子 (k, j) （向下移动）。

请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数，如果无法到达右下角格子，请你返回 -1 。

示例 1：

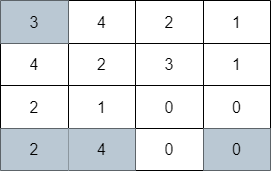
输入：grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
输出：4
解释：上图展示了到达右下角格子经过的 4 个格子。

示例 2：

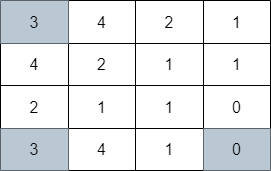
输入：grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
输出：3
解释：上图展示了到达右下角格子经过的 3 个格子。

示例 3：

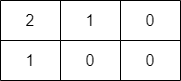
输入：grid = [[2,1,0],[1,0,0]]
输出：-1
解释：无法到达右下角格子。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10^5
• 1 <= m * n <= 10^5
• 0 <= grid[i][j] < m * n
• grid[m - 1][n - 1] == 0

题解

方法一：

思路

可以从(0,0)出发广搜到(n-1,m-1)，广搜的每个节点(x,y)需要将区间[x+1, grid[x][y]+y]和区间[y+1, grid[x][y]+x]的节点加入到队列中，但是如果队列中已经存在这些值，会造成大量重复遍历，最终超时。

所以可以将入队后的点删除，我们发现删除的点都是连续的，所以可以记录所有行和列已删除的范围，然后每次将没有删除的节点加入到队列中，每个节点只会进一次队列，而且每个节点也只会删除一次。时间复杂度$O(n*m)$。

代码

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int minimumVisitedCells(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<int> row_mx(n, -1), col_mx(m, -1);
        queue<pair<int,int>> q;
        q.emplace(0,0);
        int stp = 1;
        while (q.size()) {
            int sz = q.size();
            for (int i=0; i<sz; i++) {
                auto [x,y] = q.front(); q.pop();
                if (x == n-1 && y == m-1) return stp;
                for (int i=max(row_mx[x]+1, y+1); i<=min(y+grid[x][y], m-1); i++) {
                    q.emplace(x, i);
                    row_mx[x] = max(row_mx[x], i);
                }
                for (int i=max(col_mx[y]+1, x+1); i<=min(x+grid[x][y], n-1); i++) {
                    q.emplace(i, y);
                    col_mx[y] = max(col_mx[y], i);
                }
            }
            stp++;
        }
        return -1;
    }
};