获取所有钥匙的最短路径

题目

864. 获取所有钥匙的最短路径

---

给定一个二维网格 grid ，其中：

• ‘.’ 代表一个空房间
• ‘#’ 代表一堵墙
• ‘@’ 是起点
• 小写字母代表钥匙
• 大写字母代表锁

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 k 为 钥匙/锁 的个数，且满足 1 <= k <= 6，字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

示例 1：

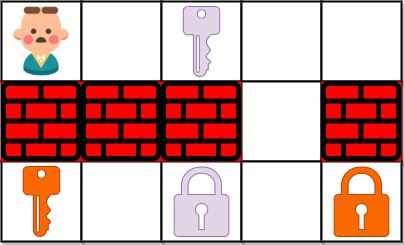
输入：grid = ["@.a.#","###.#","b.A.B"]
输出：8
解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

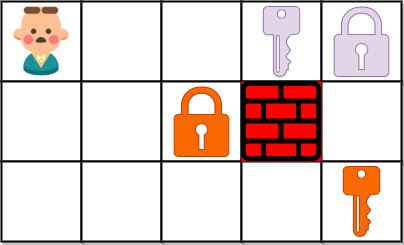
输入：grid = ["@..aA","..B#.","....b"]
输出：6

示例 3:

输入: grid = ["@Aa"]
输出: -1

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 30
• grid[i][j] 只含有 '.', '#', '@', 'a'-``'f``' 以及 'A'-'F'
• 钥匙的数目范围是 [1, 6] 
• 每个钥匙都对应一个 不同 的字母
• 每个钥匙正好打开一个对应的锁

题解

方法一：

思路

广度优先搜索。
看到求最小步数，我们想到将问题转化为图求最短路径，这里的图不是网格图是图论中的图。图论中的图由节点和边组成，这里的每个网格可以看作节点，而网格的上下左右相邻网格之间可以互通，可以看作节点之间的边，这种边是没有方向的没有权值（可以认为权值为1）的。这种无向无权图可以用广度优先搜索来做，但是需要记录之前的搜索过状态以防重复搜索导致超时。
以往我们的广搜的状态都是记录网格的位置（通过x和y两个坐标确定）。但是这个题显然不仅要记录位置信息，还要记录每把钥匙的获取情况，每把锁的开启情况。对于每一对锁和钥匙，在没有获取钥匙时是不能打开锁的，所以总共有三种情况：没有获得钥匙，获得了钥匙，获得了钥匙且开了锁。总共最多有6对钥匙与锁，所以可以使用状态压缩用一个6为3进制数表示每对钥匙与锁的获取情况。为了方便代码实现时用位运算操作，可以用6位4进制数表示，也就是12位2进制数，可以开一个三维数组vis[2^12][30][30]来表示已经经过的状态。
现在我们用status，x，y来表示一个状态
status 是6位四进制数，0表示未获取钥匙，1表示获取了钥匙，3表示获取了钥匙且开了对应锁。
x 和 y 来表示位置。
当我们移动后，变化的不仅仅是x或y，或许还有status，移动后的状态如果在此之前已经到达过，就不需要重复搜索了。另外移动到境外，移动到墙上或者移动到没有钥匙的锁上都是非法的。
每从队列中取出一个状态就检测是否获取了所有钥匙，当队列中没有状态了那么就是不可能获取所有钥匙。

代码

class Solution {
public:
    bool vis[5000][35][35];
    struct Node {
        int x, y;
        int status;
        // 6位四进制数（12位二进制数），每位四进制数对应钥匙和锁的获取情况，0未获取，1获取钥匙，3在获取钥匙的前提下解锁
        Node(int _x, int _y, int _status):x(_x),y(_y),status(_status){}
    };
    bool ok(int x, int cnt) {
        while (x) {
            if (x%2==1) cnt--;
            x>>=2;
        }
        return cnt == 0;
    }
    int new_status(int x, char ch) {
        if (ch == '#') return -1;
        if ('a' <= ch && ch <= 'f') {
            x |= 1<<(ch-'a')*2;
        }
        if ('A' <= ch && ch <= 'F') {
            if ((x>>(ch-'A')*2)%2 == 0) return -1;//无钥匙
            x |= 2<<(ch-'A')*2;
        }
        return x;
    }
    int shortestPathAllKeys(vector<string>& grid) {
        int n = grid.size(), m = grid[0].size();
        queue<Node> que;
        int sx = 0, sy = 0, key = 0;
        for (int i=0; i<n; i++) {
            for (int j=0; j<m; j++) {
                if (grid[i][j] == '@') sx = i, sy = j;
                if ('a'<=grid[i][j] && grid[i][j]<='f') key++;
            }
        }
        que.emplace(sx, sy, 0);
        vis[0][sx][sy] = true;
        int stp = 0;
        while (que.size()) {
            int sz = que.size();
            for (int i=0; i<sz; i++) {
                auto u = que.front(); que.pop();
                if (ok(u.status, key)) return stp;
                for (int j=0; j<4; j++) {
                    int x = u.x + (j-2)%2;
                    int y = u.y + (j-1)%2;
                    int status ;
                    if (x<0 || x>=n || y<0 || y>=m || 
                    (status = new_status(u.status, grid[x][y])) == -1 || vis[status][x][y]) continue;
                    vis[status][x][y] = true;
                    que.emplace(x, y, status);
                }
            }
            stp++;
        }
        return -1;
    }
};