多边形三角剖分的最低得分

题目

1039. 多边形三角剖分的最低得分

---

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。  

示例 1：

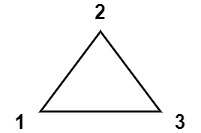
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

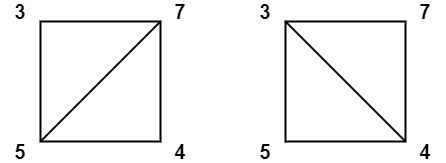
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

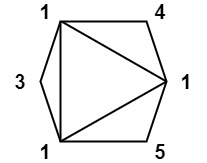
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

• n == values.length
• 3 <= n <= 50
• 1 <= values[i] <= 100

题解

方法一：

思路

容易想到拆分多边形成为更小的多边形，答案是所有拆分方式中的分数的最小值。

拆分的方法也有很多，比如对于当前多边形，找任意两个不相邻的点然后拆分成两个多边形，这两个子多边形的贡献之和作为当前拆分的分数，对于所有拆分方式中最小的分数作为当前多边形的答案。当在拆分成三角形时就不能再拆分了（递归时的终止条件）。
但是这样的的拆分方式并不好实现且不高效，拆分出的多边形的点不是连续的，比如1 2 3 4 5拆成了2 3 4和4 5 1 2。我们需要知道当前多边形所选的点，也就是一个集合作为状态的存储的数据结构。实现起来比较麻烦且状态数是n个数的子集，高达$2^n$。

现在试想一种拆分方式，对于连续的l到r的点形成的多边形形成的最小分数，记为$f_{l,r}$，最后拆分后l和r一定会与i（l<i<r）形成一个三角形，所以问题转为了求$f_{l,i}+f_{i,r}+values[l]*values[i]*values[r]$的最小值

代码

class Solution:
    def minScoreTriangulation(self, values: List[int]) -> int:
        n = len(values)
        @cache
        def dfs(l, r):
            if l+1==r: return 0
            return min(values[l]*values[r]*values[i]+dfs(l,i)+dfs(i,r) for i in range(l+1, r))
        return dfs(0, n-1)