收集所有金币可获得的最大积分

题目

100108. 收集所有金币可获得的最大积分

---

节点 0 处现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ，其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ，其中 coins[i] 表示节点 i 处的金币数量。

从根节点开始，你必须收集所有金币。要想收集节点上的金币，必须先收集该节点的祖先节点上的金币。

节点 i 上的金币可以用下述方法之一进行收集：

• 收集所有金币，得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数，你将会失去 abs(coins[i] - k) 点积分。
• 收集所有金币，得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法，节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。

返回收集 所有 树节点的金币之后可以获得的最大积分。

示例 1：

输入：edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出：11                        
解释：
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ，总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 =  11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。

示例 2：

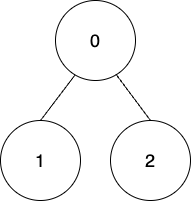
输入：edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出：16
解释：
使用第一种方法收集所有节点上的金币，因此，总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。

提示：

• n == coins.length
• 2 <= n <= 10^5
• 0 <= coins[i] <= 10^4
• edges.length == n - 1
• 0 <= edges[i][0], edges[i][1] < n
• 0 <= k <= 10^4

题解

方法一：

思路

对于每个节点，有两种选择，第二种选择会导致子树中节点的coins都减半。

可见一个节点i，其祖先使用O(logn)次第二种操作就可以让当前节点i以及它的子树coins都变为0。i子树积分最大就是0。

我们可以预处理出每个节点i减半操作j次后的coins值$c_{i,j}$。$c_{i,j+1} = \lfloor \frac{c_{i,j}}{2} \rfloor$

我们定义状态$dp_{i,j}$为第i个节点，经过j次减半操作后，i子树能获得的最大积分。

dp的转移方程显然就是两种选择中选择最大值$dp_{i,j} = max(c_{i,j}-k+\sum \limits_{s \in i’ son}dp_{s, j}, c_{i,j+1} + \sum \limits_{s \in i’ son}dp_{s, j+1})$

代码

class Solution {
public:
    int maximumPoints(vector<vector<int>>& edges, vector<int>& coins, int k) {
        int n = coins.size();
        vector<vector<int>> c(20, vector<int>(n)), dp(20, vector<int>(n, -1));
        c[0] = coins;
        for (int i=1; i<20; i++) {
            for (int j=0; j<n; j++) {
                c[i][j] = c[i-1][j]/2;
            }
        }
        
        // for (int i=0; i<31; i++) {
        //     cout << i << ": ";
        //     for (int j:c[i]) {
        //         cout << j <<  " ";
        //     }
        //     cout << endl;
        // }
        vector<vector<int>> g(n);
        for (auto& i:edges) {
            g[i[0]].push_back(i[1]);
            g[i[1]].push_back(i[0]);
        }
        
        int ans = 0;
        function<int(int,int,int)> dfs = [&](int u, int fa, int s) {
            if (dp[s][u] != -1) return dp[s][u];
            int s1 = 0, s2 = 0;
            for (int v:g[u]) {
                if (v == fa) continue;
                s1+=dfs(v, u, s);
                if (s+1<20) s2+=dfs(v, u, s+1);
            }    
            return dp[s][u] = max(c[s][u]-k+s1, c[s][u]/2+s2);
        };
        return dfs(0, -1, 0);
    }
};