最小化旅行的价格总和

题目

6378. 最小化旅行的价格总和

---

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

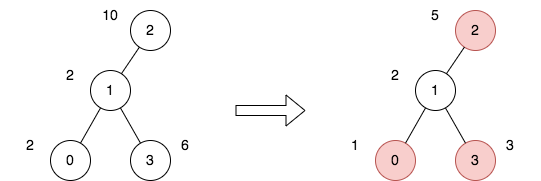
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

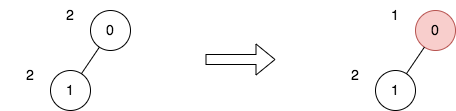
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵有效的树
• price.length == n
• price[i] 是一个偶数
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= starti, endi <= n - 1

题解

方法一：

思路

动态规划

首先需要预处理出每个点需要经过多少次。我们可以通过dfs统计每条线路经过的点i的次数w[i]。

然后我们将图中的某些的点价格减半，最后答案就是$\sum \limits_{i=0}^{n-1} price[i]*w[i]$

现在关键就在于选择哪些点价格减半。

每个点有选与不选两种情况，所以总共有$2^n$种情况，我们可以逐个判断去除选择的相邻的两个数的不合法情况，然后求出合法情况中答案最小的一个。显然在n=50的情况下，$2^50 = 1125899906842624$已经严重超时。

动态规划需要我们需要我们将问题转为同样性质的子问题，通过子问题的解较快地得到原问题的解。

既然它是一颗树，那么我们就可以指定一个点作为根（不妨设0点为根）。这样这棵树就有子问题————子树。

现在我们需要设一个状态，一般问什么就设什么。

这个题要我们求最小价格。所以可以设为每颗子树的最小价格，即f[i]为i节点及其子树的最小价值。

但是，显然这样条件还是不够，因为存在一个不能选相邻的两个节点价格减半的条件。我们的状态似乎缺失了一些信息。这时候添加一个是否选择了当前节点价格减半就可以解决问题，即f[i][j]为i节点价格是否减半（j=0否，j=1是）i节点及其子树的最小价值。

现在就考虑状态转移，也就是子问题与当前问题存在什么样的关系。

• 如果我选择了i节点价格减半，那么i节点的子节点就一定不能价格减半，即$f[i][1] = w[i]*price[i]/2+ \sum \limits _{j \in i的子节点}f[j][0]$
• 如果我没有选择了i节点价格减半，那么i节点的子节点就可以价格减半，为了价格更小，所以我们要选择减半和没有减半的状态中的最小值，即$f[i][0] = w[i]*price[i] + \sum \limits _{j \in i的子节点}min(f[j][0], f[j][1])$

现在考虑边界状态，也就是最小的子问题，防止无限的递归，这里就是叶子节点作为一颗子树。如果i是叶子，$f[i][1] = w[i]*price[i]/2, f[i][0] = w[i]*price[i]$

最后我们要求的答案就是$min(f[0][0], f[0][1])$

代码

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {
        vector<vector<int>> g(n);
        for (auto& i:edges) {
            g[i[0]].push_back(i[1]);
            g[i[1]].push_back(i[0]);
        }
        vector<int> w(n);
        function<bool(int,int,int)> dfs = [&](int u, int fa, int ta) {
            if (u == ta) {
                w[u]++;
                return true;
            }
            for (int i:g[u]) {
                if (i == fa) continue;
                if (dfs(i, u, ta)) {
                    w[u]++;
                    return true;
                }
            }
            return false;
        };
        for (auto& i:trips) {
            dfs(i[0], -1, i[1]);
        }
        // for (int i:w) cout << i << " ";
        int f[n][2];
        memset(f, 0x3f, sizeof(f));
        function<int(int,int,int)> DP = [&](int u, int fa, int c) {
            // cout << u << " " << fa << " " << c << endl;
            if (f[u][c] != INF) return f[u][c];
            if (c) {
                int res = price[u]/2*w[u];
                for (int i:g[u]) {
                    if (i == fa) continue;
                    res += DP(i, u, 0);
                }
                return f[u][c] = res;
            } else {
                int res = price[u]*w[u];
                for (int i:g[u]) {
                    if (i == fa) continue;
                    res += min(DP(i, u, 1), DP(i, u, 0));
                }
                return f[u][c] = res;
            }
        };
        return min(DP(0, -1, 0), DP(0, -1, 1));
    }
};