移除子树后的二叉树高度

题目

2458. 移除子树后的二叉树高度

---

给你一棵 二叉树 的根节点 root ，树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。

你必须在树上执行 m 个 独立 的查询，其中第 i 个查询你需要执行以下操作：

• 从树中 移除 以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不 等于根节点的值。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是执行第 i 个查询后树的高度。

注意：

• 查询之间是独立的，所以在每个查询执行后，树会回到其 初始 状态。
• 树的高度是从根到树中某个节点的 最长简单路径中的边数 。

示例 1：

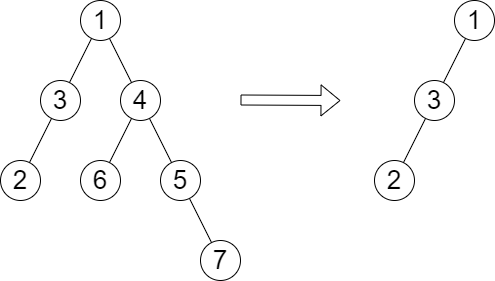
输入：root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出：[2]
解释：上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2（路径为 1 -> 3 -> 2）。

示例 2：

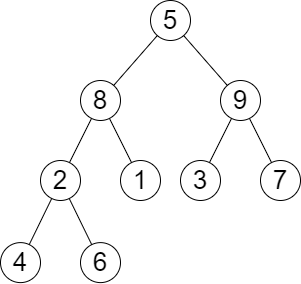
输入：root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出：[3,2,3,2]
解释：执行下述查询：
- 移除以 3 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 4）。
- 移除以 2 为根节点的子树。树的高度变为 2（路径为 5 -> 8 -> 1）。
- 移除以 4 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 6）。
- 移除以 8 为根节点的子树。树的高度变为 2（路径为 5 -> 9 -> 3）。

提示：

• 树中节点的数目是 n
• 2 <= n <= 10^5
• 1 <= Node.val <= n
• 树中的所有值 互不相同
• m == queries.length
• 1 <= m <= min(n, 10^4)
• 1 <= queries[i] <= n
• queries[i] != root.val

题解

方法一：

思路

两次 dfs
先dfs预处理出每个子树的高度。
第二次dfs直接求每个节点删除后的最大高度。
令$res_x$为删除x节点后整个树的最大高度, $d_x$为x的深度, $h_x$为x的高度
对于x左儿子节点$x_l$，$res_{x_{l}} = \max (d_x+h_{x_{r}}+1, res_x)$
对于x右儿子节点$x_r$，$res_{x_{r}} = \max (d_x+h_{x_{l}}+1, res_x)$

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int n;
    int H[100005];
    int R[100005];
    int getH(TreeNode* root) {
        if (root == nullptr) return -1;
        n = max(root->val, n);
        return H[root->val] = max(getH(root->left), getH(root->right))+1;
    }
    void getR(TreeNode* root, int lev, int res) {
        if(root == nullptr) return ;
        R[root->val] = res;
        getR(root->left, lev+1, max(res, root->right ? H[root->right->val]+lev+1 : lev));
        getR(root->right, lev+1, max(res, root->left ? H[root->left->val]+lev+1 : lev));
    }
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        getH(root);
        getR(root, 0, -1);
        for (int& i:queries) i = R[i];
        return queries;
    }
};

方法二：

思路

dfs 序
通过dfs序可以将每颗子树转化成一个区间，每个区间的第一个元素就是这个子树的根，将树上问题转成区间问题。
对于这个问题每次删除一个点后子树被删除，也就是说删除了一个子区间，我们只需要看前缀和后缀区间最深的一个节点即可。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    #define N 100005
    int tlk;
    int l[N], r[N], h[N];
    void dfs(TreeNode* root, int d) {
        if (root == nullptr) return ;
        l[root->val] = ++tlk;
        h[tlk] = d;
        dfs(root->left, d+1); dfs(root->right, d+1);
        r[root->val] = tlk;
    }
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        dfs(root, 0);
        // for (int i=1; i<=n; i++) {
        //     cout << i << " " << l[i] << ' ' << r[i] << " " << h[i] << endl;
        // }
        int n = tlk;
        vector<int> rt, lmx(n+2, 0), rmx(n+2, 0);
        for (int i=1; i<=n; i++) lmx[i] = max(lmx[i-1], h[i]);
        for (int i=n; i>=0; i--) rmx[i] = max(rmx[i+1], h[i]);
        for (int i:queries) {
            rt.push_back(max(lmx[l[i]-1], rmx[r[i]+1]));
        }
        return rt;
    }
};