并行课程 II

题目

1494. 并行课程 II

---

给你一个整数 n 表示某所大学里课程的数目，编号为 1 到 n ，数组 relations 中， relations[i] = [xi, yi]  表示一个先修课的关系，也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。

在一个学期中，你 最多 可以同时上 k 门课，前提是这些课的先修课在之前的学期里已经上过了。

请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。

示例 1：

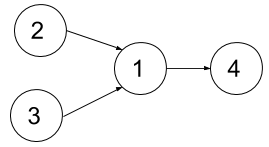
输入：n = 4, relations = [[2,1],[3,1],[1,4]], k = 2
输出：3 
解释：上图展示了题目输入的图。在第一个学期中，我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ，第三个学期上课程 4 。

示例 2：

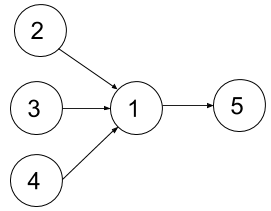
输入：n = 5, relations = [[2,1],[3,1],[4,1],[1,5]], k = 2
输出：4 
解释：上图展示了题目输入的图。一个最优方案是：第一学期上课程 2 和 3，第二学期上课程 4 ，第三学期上课程 1 ，第四学期上课程 5 。

示例 3：

输入：n = 11, relations = [], k = 2
输出：6

提示：

• 1 <= n <= 15
• 1 <= k <= n
• 0 <= relations.length <= n * (n-1) / 2
• relations[i].length == 2
• 1 <= xi, yi <= n
• xi != yi
• 所有先修关系都是不同的，也就是说 relations[i] != relations[j] 。
• 题目输入的图是个有向无环图。

题解

方法一：

思路

首先拓扑排序是错的

正解是状压dp

我们可以设计$f_S$为当前学习的课程集合为s时所需要的最小学期。且在求$f_S$时，$f_{Sub}$已经求出，$Sub \in S$.

初始化$f_{0} = 0, f_{i} = INF, i \neq 0$

对于每个$S$枚举它的子集$Sub$，当这个子集$Sub$中的课程数不超过k且不存在先修课的关系($ok_{Sub} = 1$)，另外$Sub$的前导课程$pre_{Sub}$也属于$S$集合中，那么这个集合$S$可以由学习课程集合$S-Sub$的最小学期加一个学期学习课程$Sub$转移，即$f_{S} = min(f_{S}, f_{S-Sub}+1)$

时间复杂度

总共有$2^{n}$个状态，每个状态需要枚举子集。

二进制只含一个1的状态有$n$个，每个状态有$1$个子集。

二进制只含两个1的状态有$C_{n}^{2}$个，每个状态有$2^2$个子集。

…

二进制只含k个1的状态有$C_{n}^{k}$个，每个状态有$2^k$个子集。

总枚举子集的个数是$\sum \limits_{i=0}^{n}C_{n}^{i}2^i = (1+2)^n = 3^n$

所以总时间复杂度为$O(3^n)$

代码

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int cnt1(int x) {
        int rt = 0;
        for (;x;x=x&(x-1)) rt++;
        return rt;
    }
    int minNumberOfSemesters(int n, vector<vector<int>>& relations, int k) {
        vector<int> p(n);//p[i]课程i的前导课程集合
        for (auto& i:relations) {
            p[i[1]-1] |= 1<<i[0]-1;
        }
        int sz = 1<<n;
        vector<int> pre(sz), ok(sz); 
        /*
            pre[s] 集合s是每学期学习的不超过k个的课程集合。pre[s]则是学习s这些课程所需要的前置课程。
            ok[s] 说明s中不存在先修课关系，也就是说pre[s]和s没有交集则ok[s] = true
        */
        for (int i=0; i<sz; i++) {
            // assert(__builtin_popcount(i) == cnt1(i));
            if (cnt1(i)<=k) {
                for (int j=0; j<n; j++) {
                    if (i>>j&1) {
                        pre[i] |= p[j];
                    }
                }
                ok[i] = (pre[i] & i) == 0;
            }
        }
        vector<int> f(sz, INF);
        f[0] = 0;
        for (int i=0; i<sz; i++) {
            for (int sub = i; sub; sub = i&(sub-1)) {
                if (ok[sub] && (pre[sub]|i) == i) { // sub 合法且 pre[sub]属于i
                    f[i] = min(f[i], f[i^sub]+1);
                }
            }
        }
        return f[sz-1];
    }
};