连通两组点的最小成本

题目

1595. 连通两组点的最小成本

---

给你两组点，其中第一组中有 size1 个点，第二组中有 size2 个点，且 size1 >= size2 。

任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出，其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接，则称这两组点是连通的。换言之，第一组中的每个点必须至少与第二组中的一个点连接，且第二组中的每个点必须至少与第一组中的一个点连接。

返回连通两组点所需的最小成本。

示例 1：

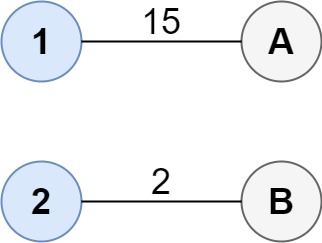
输入：cost = [[15, 96], [36, 2]]
输出：17
解释：连通两组点的最佳方法是：
1--A
2--B
总成本为 17 。

示例 2：

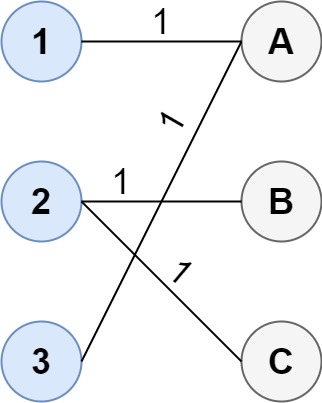
输入：cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出：4
解释：连通两组点的最佳方法是：
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意，虽然有多个点连接到第一组中的点 2 和第二组中的点 A ，但由于题目并不限制连接点的数目，所以只需要关心最低总成本。

示例 3：

输入：cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出：10

提示：

• size1 == cost.length
• size2 == cost[i].length
• 1 <= size1, size2 <= 12
• size1 >= size2
• 0 <= cost[i][j] <= 100

题解

方法一：

思路

考虑枚举第一组的前i个与第二组的选取集合j。

对于j的枚举可以从0枚举到$2^m-1$。用二进制的1代表选取情况。并且由小到大的枚举保证了当前集合的子集在之前枚举过。

现在定义状态$f_{i,j}$代表第一组的前i个与第二组的选取集合j时，所需最小成本。

初始化$f_{0,0} = 0$ 其余无穷。

$f_{i,j}$的状态转移，由于i需要选取至少一条边连接j中选取的节点。我们设j中选取了第k个点。
那么$f_{i,j} = f_{i,j\oplus k}, f_{i-1,j\oplus k}, f_{i-1, j})+cost_{i-1,k}$，$a \oplus b$ 代表a集合中移除了j元素后的子集。

代码

class Solution {
public:
    int connectTwoGroups(vector<vector<int>>& cost) {
        int n = cost.size(), m = cost[0].size();
        int f[n+1][1<<m];
        memset(f, 0x3f, sizeof(f));
        f[0][0] = 0;
        for (int i=1; i<=n; i++) {
            for (int j=0; j<1<<m; j++) {
                for (int k=0; k<m; k++) {
                    if (j>>k&1) {
                        int mn = min({f[i][j^1<<k], f[i-1][j^1<<k], f[i-1][j]})+cost[i-1][k];
                        f[i][j] = min(f[i][j], mn);
                    }
                }   
            }
        }
        // for (int i=1; i<=n; i++) {
        //     for (int j=0; j<1<<m; j++) {
        //         cout << i << " " << j << " " << f[i][j] << "\n";
        //     }
        // }
        return f[n][(1<<m)-1];
    }
};