矩阵中严格递增的单元格数

题目

6456. 矩阵中严格递增的单元格数

---

给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat，你可以选择任一单元格作为 起始单元格 。

从起始单元格出发，你可以移动到 同一行或同一列 中的任何其他单元格，但前提是目标单元格的值 严格大于 当前单元格的值。

你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。

请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。

返回一个表示可访问单元格最大数量的整数。

示例 1：

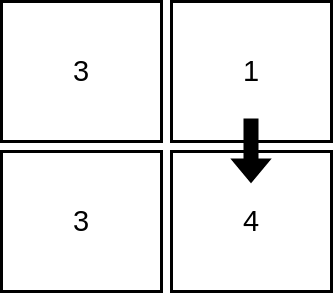
输入：mat = [[3,1],[3,4]]
输出：2
解释：上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。

示例 2：

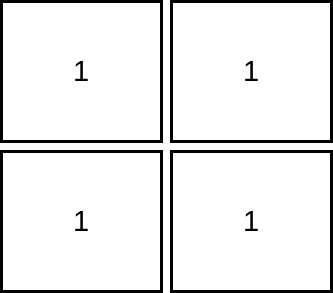
输入：mat = [[1,1],[1,1]]
输出：1
解释：由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。

示例 3：

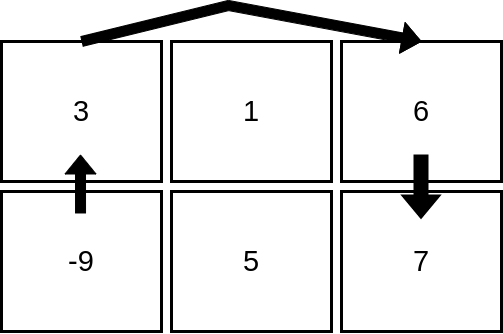
输入：mat = [[3,1,6],[-9,5,7]]
输出：4
解释：上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。

提示：

• m == mat.length 
• n == mat[i].length 
• 1 <= m, n <= 10^5
• 1 <= m * n <= 10^5
• -10^5 <= mat[i][j] <= 10^5

题解

方法一：

思路

动态规划

只需要找到mat中每个值mat[i][j]作为移动终点的步数，记为状态$f_{i,j}$。答案就是所有状态中的最大值。

关键在于状态的转移。

根据题意，对于mat[i][j]，我们可以移动到第i行中比mat[i][j]大的位置上，实际上我们移动到这一行中比mat[i][j]大的最小元素就行。但是要注意这个最小元素在这一行中可能有多个。对于列也同样如此。

考虑$f_{i,j}$由哪些状态转移而来，如果我们按照mat[i][j]由小到大的顺序求状态值，那么显然在求$f_{i,j}$时，第i行中f最大值和第j行中f最大值都可以转移到$f_{i,j}$。所以可以用一个长度为n的数组rf来记录每一行的最大值；用一个长度为m的数组cf来记录每一列的最大值。这两个数组的只有等到相同的mat值的状态都更新后才更新。

代码

class Solution {
public:
    int maxIncreasingCells(vector<vector<int>>& mat) {
        map<int,vector<pair<int,int>>> mp;
        int n = mat.size(), m = mat[0].size();
        for (int i=0; i<n; i++) {
            for (int j=0; j<m; j++) {
                mp[mat[i][j]].emplace_back(i,j);
            }
        }
        vector<vector<int>> f(n, vector<int>(m, 0)); // f[i][j] (i,j)作为移动的终点 所能访问的单元格数
        vector<int> rf(n), cf(m); // rf[i] 第i行的最大f值, f[i][j] = max(rf[i], cf[i])+1;
        int ans = 0;
        for (auto& [i,j]:mp) {
            for (auto [x,y]:j) {
                f[x][y] = max(rf[x], cf[y])+1;
                ans = max(f[x][y], ans);
            }
            for (auto [x,y]:j) {
                rf[x] = max(rf[x], f[x][y]);
                cf[y] = max(cf[y], f[x][y]);
            }
        }
        return ans;
    }
};

方法二：

思路

另一种思路，可以将问题转化为图论问题。

这个问题关键在于状态转移时可能会超时。
我们构造一个极端案例在一行中有a个1和b个2，对于b个2的状态都可以由a个1的转台转移而来。时间复杂度O(ab)。但是如果建立一个虚拟节点状态在让a个1都转移到虚拟节点，然后虚拟节点再转移到b个2.这样时间复杂度O(a+b)

代码

todo