灌溉花园的最少水龙头数目

题目

1326. 灌溉花园的最少水龙头数目

---

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i -  ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

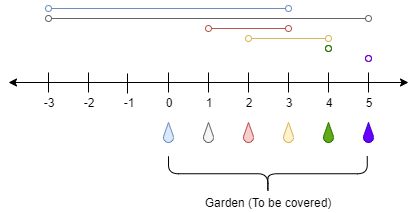
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

提示：

• 1 <= n <= 10^4
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

题解

方法一：

思路

我们可以设$f_i$为从0到i需要多少个水龙头，初始化$f_0 = 0, f_i=\infty, i>0$

然后求出每个水龙头的浇灌范围，并进行排序，我们按照能浇灌的最右端升序排序，以便保证dp转移时无后效性。

对已排序的水龙头v遍历，设在遍历第i个水龙头时水龙头的左端为$l_i$，右端为$r_i$，那么有状态转移$f_{r_i} = min(f_{r_i}, f_{l_i}+1)$

若最后$f_n = \infty$则无法到达。

时间复杂度$O(nlogn)$

代码

class Solution {
public:
    int minTaps(int n, vector<int>& ranges) {
        vector<pair<int,int>> v;
        for (int i=0; i<=n; i++) {
            v.emplace_back(max(0,i-ranges[i]), min(n, i+ranges[i]));
        }
        sort(v.begin(), v.end());
        int INF = 0x3f3f3f3f;
        vector<int> f(n+1, INF);
        f[0] = 0;
        for (int i=0; i<=n; i++) {
            // if (i>0&&v[i-1].second == v[i].second) continue;
            auto [x, y] = v[i];
            for (int j=x+1; j<=y; j++) {
                f[j] = min(f[j], f[x]+1);
            }
        }
        return f[n] == INF?-1:f[n];
    }
};

方法二：

思路

可以预处理出每个点i能到达的最右端r[i]。

我们从左端开始考虑一个最大的覆盖范围的水龙头，然后在这个范围内寻找能覆盖最远的水龙头。贪心即可。

代码

class Solution {
public:
    int minTaps(int n, vector<int>& ranges) {
        vector<int> r(n+1, 0); // r[i] i点最大能覆盖到r[i]
        for (int i=0; i<=n; i++) {
            int x = max(0, i-ranges[i]), y = i+ranges[i];
            r[x] = max(r[x], y);
        }
        int ans = 0, mx = 0, cur = 0;
        for (int i=0; i<n; i++) {
            mx = max(mx, r[i]);
            if (cur == i) {
                if (cur == mx) return -1;
                cur = mx;
                ans++;
            }
        }
        return ans;
    }
};