Hot Start Up (easy version)
现在由k种程序
在一个cpu中如果执行了第$i$种和然后又执行第$i$种程序，则花费$hot_i$时间。否则是$cold_i$时间
现在有一个长度为n的需要执行的程序序列。有两个cpu，两个cpu只能同时运行一个。
运行完所有程序所需要的时间是多少。
0%
Coloring Brackets
一对对应的括号只能涂其中一个括号
任意相邻的两个有颜色的括号颜色不能相同
涂的颜色只有两种，红色或蓝色
给出一个合法括号序列（每个左括号都有对应的右括号）
现在你需要给这个括号序列涂上颜色。
涂色的规则:
求合法涂色的方案数。
从仓库到码头运输箱子
portsi表示第i个箱子需要送达的码头，weightsi是第i个箱子的重量。portsCount是码头的数目。maxBoxes和maxWeight分别是卡车每趟运输箱子数目和重量的限制。卡车从
boxes队列中按顺序取出若干个箱子，但不能违反maxBoxes和maxWeight限制。对于在卡车上的箱子，我们需要 按顺序 处理它们，卡车会通过 一趟行程 将最前面的箱子送到目的地码头并卸货。如果卡车已经在对应的码头，那么不需要 额外行程 ，箱子也会立马被卸货。
卡车上所有箱子都被卸货后，卡车需要 一趟行程 回到仓库，从箱子队列里再取出一些箱子。
- 卡车将所有箱子装上车，到达码头 1 ，然后去码头 2 ，然后再回到码头 1 ，最后回到仓库，总共需要 4 趟行程。
卡车首先运输第一个箱子，到达码头 1 ，然后回到仓库，总共 2 趟行程。
卡车运输第二、第三、第四个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
卡车运输第五个箱子，到达码头 2 ，回到仓库，总共 2 趟行程。
卡车运输第一和第二个箱子，到达码头 1 ，然后回到仓库，总共 2 趟行程。
卡车运输第三和第四个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
卡车运输第五和第六个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
卡车运输第一个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
卡车运输第二个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
卡车运输第三和第四个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
卡车运输第五个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
卡车运输第六和第七个箱子，到达码头 3 ，然后去码头 4 ，然后回到仓库，总共 3 趟行程。
卡车运输第八和第九个箱子，到达码头 1 ，然后去码头 5 ，然后回到仓库，总共 3 趟行程。
1 <= boxes.length <= 10^51 <= portsCount, maxBoxes, maxWeight <= 10^51 <= portsi <= portsCount1 <= weightsi <= maxWeight
你有一辆货运卡车，你需要用这一辆车把一些箱子从仓库运送到码头。这辆卡车每次运输有 箱子数目的限制 和 总重量的限制 。
给你一个箱子数组 boxes 和三个整数 portsCount, maxBoxes 和 maxWeight ，其中 boxes[i] = [portsi, weighti] 。
箱子需要按照 数组顺序 运输，同时每次运输需要遵循以下步骤：
卡车在将所有箱子运输并卸货后，最后必须回到仓库。
请你返回将所有箱子送到相应码头的 最少行程 次数。
示例 1：
```txt
输入：boxes = [[1,1],[2,1],[1,1]], portsCount = 2, maxBoxes = 3, maxWeight = 3
输出：4
解释：最优策略如下：
所以总行程数为 4 。
注意到第一个和第三个箱子不能同时被卸货，因为箱子需要按顺序处理（也就是第二个箱子需要先被送到码头 2 ，然后才能处理第三个箱子）。
```
示例 2：
```txt
输入：boxes = [[1,2],[3,3],[3,1],[3,1],[2,4]], portsCount = 3, maxBoxes = 3, maxWeight = 6
输出：6
解释：最优策略如下：
总行程数为 2 + 2 + 2 = 6 。
```
示例 3：
```txt
输入：boxes = [[1,4],[1,2],[2,1],[2,1],[3,2],[3,4]], portsCount = 3, maxBoxes = 6, maxWeight = 7
输出：6
解释：最优策略如下：
总行程数为 2 + 2 + 2 = 6 。
```
示例 4：
```txt
输入：boxes = [[2,4],[2,5],[3,1],[3,2],[3,7],[3,1],[4,4],[1,3],[5,2]], portsCount = 5, maxBoxes = 5, maxWeight = 7
输出：14
解释：最优策略如下：
总行程数为 2 + 2 + 2 + 2 + 3 + 3 = 14 。
```
提示：
灌溉花园的最少水龙头数目
1 <= n <= 10^4ranges.length == n + 10 <= ranges[i] <= 100
在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。
花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。
示例 1：
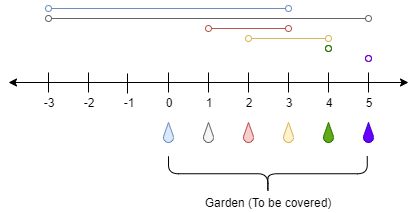
```txt
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
```
示例 2：
```txt
输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。
```
提示：
给墙壁刷油漆
一位需要 付费 的油漆匠，刷第
i堵墙需要花费time[i]单位的时间，开销为cost[i]单位的钱。一位 免费 的油漆匠，刷 任意 一堵墙的时间为
1单位，开销为0。但是必须在付费油漆匠 工作 时，免费油漆匠才会工作。1 <= cost.length <= 500cost.length == time.length1 <= cost[i] <= 10^61 <= time[i] <= 500
给你两个长度为 n 下标从 0 开始的整数数组 cost 和 time ，分别表示给 n 堵不同的墙刷油漆需要的开销和时间。你有两名油漆匠：
请你返回刷完 n 堵墙最少开销为多少。
示例 1：
```txt
输入：cost = [1,2,3,2], time = [1,2,3,2]
输出：3
解释：下标为 0 和 1 的墙由付费油漆匠来刷，需要 3 单位时间。同时，免费油漆匠刷下标为 2 和 3 的墙，需要 2 单位时间，开销为 0 。总开销为 1 + 2 = 3 。
```
示例 2：
```txt
输入：cost = [2,3,4,2], time = [1,1,1,1]
输出：4
解释：下标为 0 和 3 的墙由付费油漆匠来刷，需要 2 单位时间。同时，免费油漆匠刷下标为 1 和 2 的墙，需要 2 单位时间，开销为 0 。总开销为 2 + 2 = 4 。
```
提示：
K 次调整数组大小浪费的最小总空间
1 <= nums.length <= 2001 <= nums[i] <= 10^60 <= k <= nums.length - 1
你正在设计一个动态数组。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是 i 时刻数组中的元素数目。除此以外，你还有一个整数 k ，表示你可以 调整 数组大小的 最多 次数（每次都可以调整成 任意 大小）。
t 时刻数组的大小 sizet 必须大于等于 nums[t] ，因为数组需要有足够的空间容纳所有元素。t 时刻 浪费的空间 为 sizet - nums[t] ，总 浪费空间为满足 0 <= t < nums.length 的每一个时刻 t 浪费的空间 之和 。
在调整数组大小不超过 k 次的前提下，请你返回 最小总浪费空间 。
注意：数组最开始时可以为 任意大小 ，且 不计入 调整大小的操作次数。
示例 1：
```txt
输入：nums = [10,20], k = 0
输出：10
解释：size = [20,20].
我们可以让数组初始大小为 20 。
总浪费空间为 (20 - 10) + (20 - 20) = 10 。
```
示例 2：
```txt
输入：nums = [10,20,30], k = 1
输出：10
解释：size = [20,20,30].
我们可以让数组初始大小为 20 ，然后时刻 2 调整大小为 30 。
总浪费空间为 (20 - 10) + (20 - 20) + (30 - 30) = 10 。
```
示例 3：
```txt
输入：nums = [10,20,15,30,20], k = 2
输出：15
解释：size = [10,20,20,30,30].
我们可以让数组初始大小为 10 ，时刻 1 调整大小为 20 ，时刻 3 调整大小为 30 。
总浪费空间为 (10 - 10) + (20 - 20) + (20 - 15) + (30 - 30) + (30 - 20) = 15 。
```
提示：
母函数
- 母函数